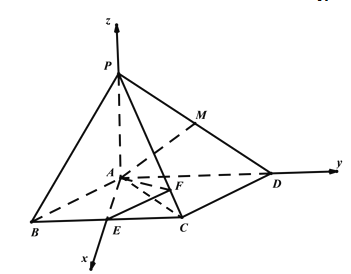
题目内容
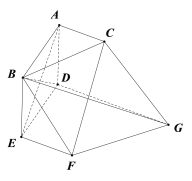
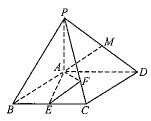
【题目】已知,如图四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,E,M分别是BC,PD中点,点F在棱PC上移动.
,E,M分别是BC,PD中点,点F在棱PC上移动.
(1)证明无论点F在PC上如何移动,都有平面![]() 平面
平面![]() ;
;
(2)当直线AF与平面PCD所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)易证得![]() ,
,![]() ,即证得
,即证得![]() 平面
平面![]() ,进而证得结论.
,进而证得结论.
(2) 以AE,AD,AP所在直线分别为x轴,y轴,z轴建立坐标系,设![]() ,根据向量法求出线面成角的正弦值,求出取最大值时的参数
,根据向量法求出线面成角的正弦值,求出取最大值时的参数![]() ,依次求出法向量即可得出结果.
,依次求出法向量即可得出结果.
(1)连接AC.
![]() 底面ABCD为菱形,
底面ABCD为菱形,![]() ,
,
![]() 是正三角形,
是正三角形,![]() 是BC中点,
是BC中点,
![]() ,又
,又![]() ,
,
![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(2)由(1)知,AE,AD,AP两两垂直,
以AE,AD,AP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
易知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
而![]()
且![]() ,
,
设平面PCD的法向量![]() ,
,
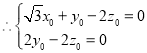 ,取
,取![]() ,
,
![]() .根据题意,
.根据题意,
线面角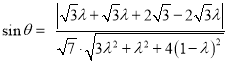
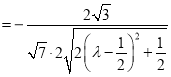
当![]() 时,
时,![]() 最大,
最大,
此时F为PC的中点,即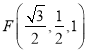 ,
,
![]() ,
,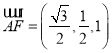 ,
,![]() .
.
设平面AEF的法向量为![]() ,
,
平面AEM的法向量为![]() ,
,
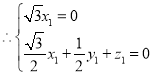 ,解得
,解得![]() ,
,
同理可得![]() ,
,
![]() ,
,
所以二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
【题目】2014年非洲爆发了埃博拉病毒疫情,在疫情结束后,当地防疫部门做了一项回访调查,得到如下结果,
患病 | 不患病 | |
有良好卫生习惯 | 20 | 180 |
无良好卫生习惯 | 80 | 220 |
(1)结合上面列联表,是否有![]() 的把握认为是否患病与卫生习惯有关?
的把握认为是否患病与卫生习惯有关?
(2)现从有良好卫生习惯且不患病的180人中抽取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共5人,再从这5人中选两人给市民做健康专题报告,求
共5人,再从这5人中选两人给市民做健康专题报告,求![]() ,
,![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |