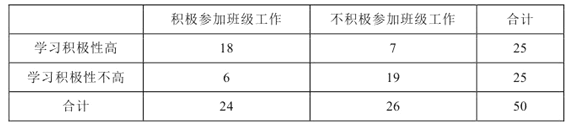
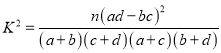题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)给出![]() 的一个取值,使得曲线
的一个取值,使得曲线![]() 存在斜率为
存在斜率为![]() 的切线,并说明理由;
的切线,并说明理由;
(Ⅱ)若![]() 存在极小值和极大值,证明:
存在极小值和极大值,证明: ![]() 的极小值大于极大值.
的极小值大于极大值.
【答案】(I)详见解析;(II)详见解析.
【解析】试题分析:(Ⅰ)先对原函数求导,只需令方程![]() 有解即可得
有解即可得![]() 的范围,进而可得
的范围,进而可得![]() 的一个取值,在验证即可;(Ⅱ)对
的一个取值,在验证即可;(Ⅱ)对![]() 求导;求方程
求导;求方程![]() 的所有实数根,列表格判断各个根左右两边符合。进而可得结果.
的所有实数根,列表格判断各个根左右两边符合。进而可得结果.
试题解析:(Ⅰ)函数![]() 的定义域是
的定义域是![]() 且
且![]() ,且
,且![]() .
.
当![]() 时,曲线
时,曲线![]() 存在斜率为
存在斜率为![]() 的切线.证明如下:
的切线.证明如下:
曲线![]() 存在斜率为
存在斜率为![]() 的切线
的切线![]() 方程
方程![]() 存在
存在![]() 上的解,
上的解,
令![]() ,整理得
,整理得![]() ,
,
解得![]() ,或
,或![]() .
.
所以,当![]() 时,曲线
时,曲线![]() 存在斜率为
存在斜率为![]() 的切线.
的切线.
注:本题答案不唯一,只要![]() 均符合要求.
均符合要求.
(Ⅱ)由(Ⅰ)得![]() .
.
①当![]() 时,
时, ![]() 恒成立,
恒成立,
函数![]() 在区间
在区间![]() 和
和![]() 上单调递增,无极值,不合题意.
上单调递增,无极值,不合题意.
②当![]() 时,令
时,令![]() ,整理得
,整理得![]() .
.
由![]() ,
,
所以,上述方程必有两个不相等的实数解![]() ,
, ![]() ,不妨设
,不妨设![]() .
.
由![]() 得
得![]() .
.
![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
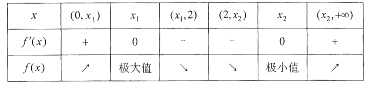
所以, ![]() 存在极大值
存在极大值![]() ,极小值
,极小值![]() .
.
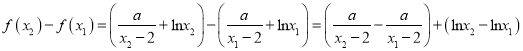 .
.
因为![]() ,且
,且![]() .
.
所以![]() ,
, ![]() ,
,
所以![]() .
.
所以![]() 的极小值大于极大值.
的极小值大于极大值.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
【题目】漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资.
(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量![]() (单位:粒,
(单位:粒, ![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量![]() (单位:粒),整理得下表:
(单位:粒),整理得下表:
雕刻量 | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天的收入不低于300元的概率.