题目内容
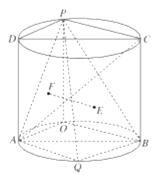
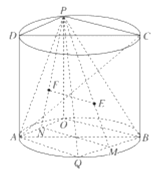
【题目】如图,圆柱的轴截面![]() 是边长为2的正方形,点P是圆弧
是边长为2的正方形,点P是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),点Q是圆弧
重合),点Q是圆弧![]() 的中点,且点
的中点,且点![]() 在平面
在平面![]() 的两侧.
的两侧.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设点P在平面![]() 上的射影为点O,点
上的射影为点O,点![]() 分别是
分别是![]() 和
和![]() 的重心,当三棱锥
的重心,当三棱锥![]() 体积最大时,回答下列问题.
体积最大时,回答下列问题.
(i)证明:![]() 平面
平面![]() ;
;
(ii)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)(i)证明见解析(ii)![]()
【解析】
(1)由![]() ,
,![]() 可得
可得![]() 平面
平面![]() ,即可证明;
,即可证明;
(2)(i)连接![]() 并延长交
并延长交![]() 于点M,连接
于点M,连接![]() 并延长交
并延长交![]() 于点N,连接
于点N,连接![]() ,利用平行线分线段成比例可得
,利用平行线分线段成比例可得![]() ,即可得
,即可得![]() 得证;
得证;
(ii)根据![]() 即可求解.
即可求解.
(1)证明:因为![]() 是轴截面,
是轴截面,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
又点P是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),且
重合),且![]() 为直径,
为直径,
所以![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() .
.
(2)当三棱锥![]() 体积最大时,点P为圆弧
体积最大时,点P为圆弧![]() 的中点.所以点O为圆弧
的中点.所以点O为圆弧![]() 的中点,
的中点,
所以四边形![]() 为正方形,且
为正方形,且![]() 平面
平面![]() .
.
(i)证明:连接![]() 并延长交
并延长交![]() 于点M,连接
于点M,连接![]() 并延长交
并延长交![]() 于点N,连接
于点N,连接![]() ,
,
则![]() ,
,
因为![]() 分别为三角形的重心,所以
分别为三角形的重心,所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(ii)因为![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,即
,即![]() 是三棱锥
是三棱锥![]() 的高.
的高.
又![]() ,
,![]() ,
,
所以![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.

(1)用样本估计总体,以频率作为概率,若在![]() 两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: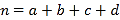 ,其中
,其中![]() )
)
【题目】某农场为了提高某品种水稻的产量,进行良种优选,在同一试验田中分两块种植了甲乙两种水稻.为了比较甲乙两种水稻的产量,现从甲乙两种水稻中各随机选取20株成熟水稻.根据每株水稻颗粒的重量(单位:克)绘制了如下茎叶图:
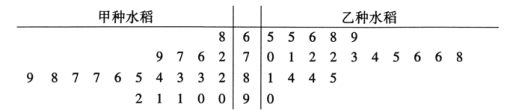
(1)根据茎叶图判断哪种水稻的产量更高?并说明理由;
(2)求40株水稻颗粒重量的中位数![]() ,并将重量超过
,并将重量超过![]() 和不超过
和不超过![]() 的水稻株数填入下面的列联表:
的水稻株数填入下面的列联表:
超过 | 不超过 | |
甲种水稻 | ||
乙种水稻 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种水稻的产量有差异?附:
的把握认为两种水稻的产量有差异?附: ;
;
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |