题目内容
【题目】已知椭圆E:![]() 的焦距为2
的焦距为2![]() ,一条准线方程为x=
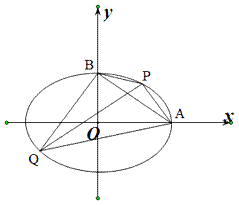
,一条准线方程为x=![]() ,A,B分别为椭圆的右顶点和上顶点,点P,Q在的椭圆上,且点P在第一象限.
,A,B分别为椭圆的右顶点和上顶点,点P,Q在的椭圆上,且点P在第一象限.
(1)求椭圆E的标准方程;
(2)若点P,Q关于坐标原点对称,且PQ⊥AB,求四边形ABCD的面积;
(3)若AP,BQ的斜率互为相反数,求证:PQ斜率为定值.
【答案】(1)![]() (2)
(2)![]() (3)见证明
(3)见证明
【解析】
(1)由焦距得c,再由准线方程结合a2=b2+c2,可得椭圆方程;(2)![]() ,由题意可得kPQ=2,即直线PQ方程为y=2x,与椭圆方程联立解得|PQ|,可得四边形ABCD的面积;(3)设直线AP的斜率为k(k<0),则直线AP方程y=k(x-2),与椭圆方程联立得P点坐标,利用直线AN斜率与AM斜率互为相反数,将k换为-k,可求N的坐标,再利用斜率计算公式即可得出PQ斜率为定值.
,由题意可得kPQ=2,即直线PQ方程为y=2x,与椭圆方程联立解得|PQ|,可得四边形ABCD的面积;(3)设直线AP的斜率为k(k<0),则直线AP方程y=k(x-2),与椭圆方程联立得P点坐标,利用直线AN斜率与AM斜率互为相反数,将k换为-k,可求N的坐标,再利用斜率计算公式即可得出PQ斜率为定值.
(1)由题意可得:![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为:
的标准方程为:![]() .
.
(2) ![]() ,
,
![]() 点
点![]() 关于坐标原点对称,且
关于坐标原点对称,且![]() ,
,
![]() .可得直线
.可得直线![]() 的方程为:
的方程为:![]() .
.
联立![]() ,解得
,解得![]() ,
,![]() .
.
![]() .
.
![]() 四边形
四边形![]() 的面积
的面积![]() .
.
(3)证明:设![]() ,
, ![]() .
.
设直线![]() 的斜率为
的斜率为![]() ,
, ![]() ,则直线方程为:
,则直线方程为:![]() ,
,
联立![]() ,化为:
,化为:![]() ,
,
![]() ,解得
,解得![]() ,
,![]() .
.
![]() 的斜率互为相反数,
的斜率互为相反数, ![]() 直线
直线![]() 的斜率为
的斜率为![]() ,直线方程为:
,直线方程为:![]() .
.
联立![]() ,化为:
,化为:![]() ,
,
![]() ,
,![]() .
.
![]() 斜率
斜率 为定值.
为定值.

练习册系列答案
相关题目