题目内容
已知等差数列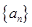 的首项
的首项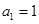 ,公差
,公差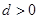 ,数列
,数列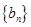 是等比数列,且
是等比数列,且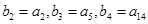 .
.
(1)求数列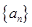 和
和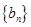 的通项公式;
的通项公式;
(2)设数列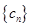 对任意正整数n,均有
对任意正整数n,均有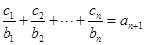 成立,求
成立,求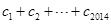 的值.
的值.
(1)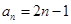 ,
, 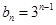 ; (2)
; (2)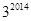 .
.
解析试题分析:(1)由已知可首先求得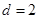 ,进一步得
,进一步得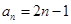 ;
;
根据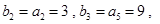 得到
得到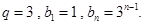
(2)从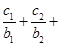
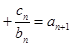 ①出发,得到
①出发,得到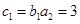 ,
,
再据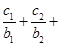 +
+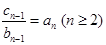 ②
②
①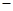 ②,得
②,得 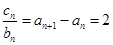 , 从而可得
, 从而可得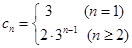 ,
,
从第二项起利用等比数列的求和公式.
(1)∵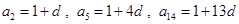 ,且
,且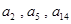 成等比数列,
成等比数列,
∴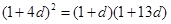 ,解得,
,解得,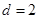 , 2分
, 2分
∴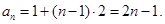 4分
4分
又∵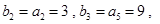 ∴
∴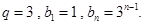 6分
6分
(2)∵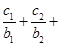
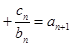 , ①
, ①
∴ ,即
,即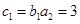 , 7分
, 7分
又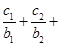 +
+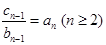 , ②
, ②
①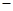 ②,得
②,得 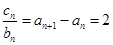 ,
,
∴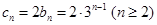 ,∴
,∴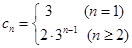 , 10分
, 10分
则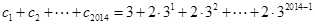
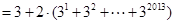
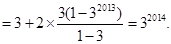 12分
12分
考点:等差数列、等比数列的通项公式,数列的求和.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
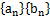 (
(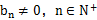 ),满足
),满足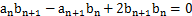 .
.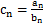 ,求数列
,求数列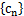 的通项公式;
的通项公式;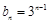 ,求数列
,求数列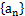 的前n项和
的前n项和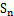
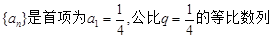 ,设数列
,设数列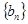 满足
满足 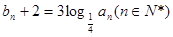 .
.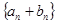 的前
的前 项和为
项和为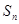 ;
; ,若
,若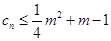 对一切正整数
对一切正整数 的取值范围.
的取值范围.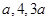 ,前
,前 项的和为
项的和为 .
.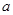 ;
;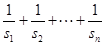
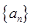 中,
中,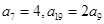 .
.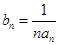 ,求数列
,求数列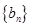 的前
的前 项和
项和 .
.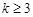 ,若项数为
,若项数为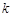 的数列
的数列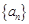 满足:对任意的
满足:对任意的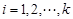 ,均有
,均有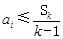 (其中
(其中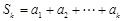 ),则称数列
),则称数列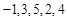 和
和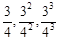 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由;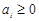 对
对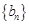 是公差为
是公差为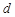 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数 ,
,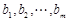
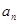 }、{
}、{  }满足:
}满足: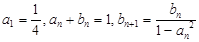 .
.
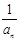 }为等差数列,并求数列
}为等差数列,并求数列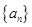 和{
和{  ,求实数
,求实数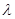 为何值时
为何值时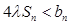 恒成立.
恒成立.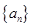 的首项
的首项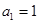 ,公差
,公差 ,且
,且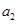 、
、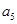 、
、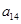 分别是等比数列
分别是等比数列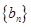 的
的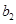 、
、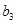 、
、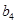 .
.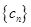 对任意正整数
对任意正整数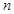 均有
均有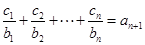 成立,求
成立,求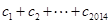 的值.
的值.