题目内容
(2013•南京二模)已知圆锥的侧面展开图是一个半径为3cm,圆心角为
π的扇形,则此圆锥的高为
| 2 |
| 3 |
2
| 2 |
2
cm.| 2 |
分析:设此圆的底面半径为r,高为h,母线为l,根据底面圆周长等于展开扇形的弧长,建立关系式解出r=1,再根据勾股定理得h=
=2
cm,即得此圆锥高的值.
| l2-r2 |
| 2 |
解答:解:设此圆的底面半径为r,高为h,母线为l,则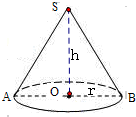
∵圆锥的侧面展开图是一个半径为3cm,圆心角为
π的扇形,
∴l=3,得2πr=
×l=2π,解之得r=1
因此,此圆锥的高h=
=
=2
cm
故答案为:2

∵圆锥的侧面展开图是一个半径为3cm,圆心角为
| 2 |
| 3 |
∴l=3,得2πr=
| 2π |
| 3 |
因此,此圆锥的高h=
| l2-r2 |
| 32-12 |
| 2 |
故答案为:2
| 2 |
点评:本题给出圆锥的侧面展开图扇形的半径为和圆心角,求圆锥高的大小.着重考查了圆锥的定义与性质和旋转体侧面展开等知识,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
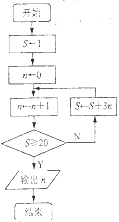 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是