题目内容
要证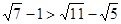 ,只需证
,只需证 ,即需
,即需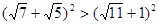 ,即需证
,即需证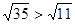 ,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
| A.比较法 | B.综合法 | C.分析法 | D.反证法 |
C
解析试题分析:根据题意,从结论出发来寻找命题成立的充分条件,可知为分析法,由于要证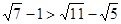 ,只需证
,只需证 ,即需
,即需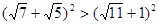 ,即需证
,即需证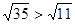 ,即证35>11,因为35>11显然成立,所以原不等式成立,是执果索引,故选C.
,即证35>11,因为35>11显然成立,所以原不等式成立,是执果索引,故选C.
考点:分析法
点评:主要是考查了不等式的证明方法的运用,属于基础题。

练习册系列答案
相关题目
已知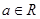 ,不等式
,不等式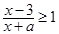 的解集为
的解集为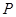 ,且
,且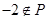 ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A.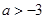 | B.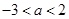 |
C.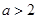 或 或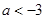 | D.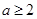 或 或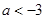 |
对数函数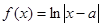 在
在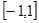 区间上恒有意义,则
区间上恒有意义,则 的取值范围是( )
的取值范围是( )
A.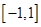 | B.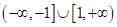 |
C.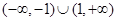 | D.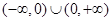 |
不等式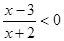 的解集是 ( )
的解集是 ( )
A.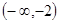 | B.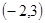 | C. | D. |
若函数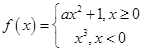 ,则不等式
,则不等式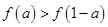 的解集为( )
的解集为( )
A. | B.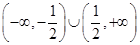 |
C.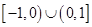 | D.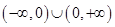 |
若不等式x2+ax+1³0对于一切xÎ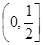 恒成立,则a的最小值是 ( )
恒成立,则a的最小值是 ( )
| A.0 | B.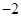 | C.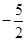 | D.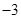 |
设 小于0,则3个数:
小于0,则3个数: ,
,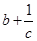 ,
,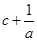 的值 ( )
的值 ( )
| A.至多有一个不小于-2 | B.至多有一个不大于2 |
| C.至少有一个不大于-2 | D.至少有一个不小于2 |
已知 ,则2a+3b的取值范围是( )
,则2a+3b的取值范围是( )
A. | B.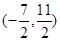 | C. | D.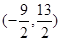 |
当m>1时,关于x的不等式x2+(m-1)x-m≥0的解集是
| A.{x|x≤1,或x≥-m} | B. {x|1≤x≤-m } |
| C.{x|x≤-m,或x≥1} | D. {x|-m≤x≤1 } |