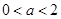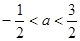题目内容
若函数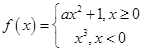 ,则不等式
,则不等式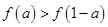 的解集为( )
的解集为( )
A. | B.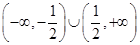 |
C.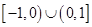 | D.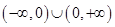 |
B
解析试题分析: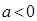 时,
时,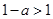 ,
,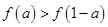 即
即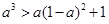 ,解得,
,解得,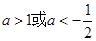 ,所以,
,所以,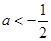 ;
;
a=0时,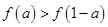 即1>a+1,不合题意;
即1>a+1,不合题意;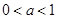 时,
时,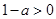 ,
,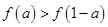 即
即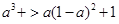 ,解得,
,解得,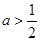 ,
,
所以,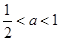 ;
;
a=1时,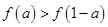 即a+1>1恒成立;
即a+1>1恒成立; 时,
时,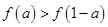 即
即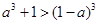 ,化简得,
,化简得, 恒成立,所以,
恒成立,所以, ;
;
综上知,不等式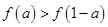 的解集为
的解集为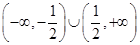 ,选B。
,选B。
考点:分段函数的概念,一元二次不等式解法,分类讨论思想。
点评:中档题,对于抽象函数构成的不等式,应首先考虑“具体化”,本题通过分类讨论,转化得到几个不同的简单不等式。作为选择题,可结代入验证的方法,排除错误选项。

练习册系列答案
相关题目
不等式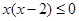 的解集是( )
的解集是( )
A.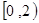 | B.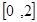 |
C.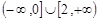 | D.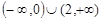 |
不等式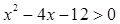 的解集是
的解集是
A.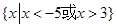 | B.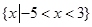 |
C.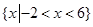 | D.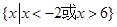 |
若不等式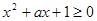 对任意
对任意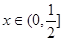 成立,则
成立,则 的最小值为( )
的最小值为( )
| A.0 | B.-2 | C.-3 | D.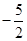 |
a∈R,且a2+a<0,那么-a,-a3,a2的大小关系是( )
| A.a2>-a3>-a | B.-a>a2>-a3 |
| C.-a3>a2>-a | D.a2>-a>-a3 |
要证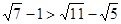 ,只需证
,只需证 ,即需
,即需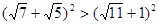 ,即需证
,即需证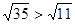 ,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
| A.比较法 | B.综合法 | C.分析法 | D.反证法 |
二次不等式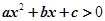 的解集是全体实数的条件是 ( )
的解集是全体实数的条件是 ( )
A.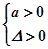 | B.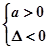 | C.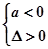 | D.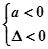 |
不等式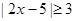 的解集为( )
的解集为( )
A.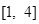 | B.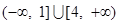 |
C.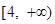 | D.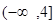 |
 :x
:x