题目内容
当m>1时,关于x的不等式x2+(m-1)x-m≥0的解集是
| A.{x|x≤1,或x≥-m} | B. {x|1≤x≤-m } |
| C.{x|x≤-m,或x≥1} | D. {x|-m≤x≤1 } |
C
解析试题分析:根据题意可知,原不等式可化为 (x+m)(x-1)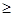 0,结合一元二次不等式的解法,求出它的解集,解得为
0,结合一元二次不等式的解法,求出它的解集,解得为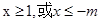 ,因此可知结论为{x|x≤-m,或x≥1},选C.
,因此可知结论为{x|x≤-m,或x≥1},选C.
考点:不等式的解集
点评:本题主要考查一元二次不等式的解法,属于基础题

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
要证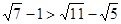 ,只需证
,只需证 ,即需
,即需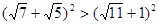 ,即需证
,即需证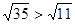 ,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
| A.比较法 | B.综合法 | C.分析法 | D.反证法 |
若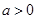 ,使不等式
,使不等式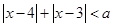 在
在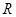 上的解集不是空集的
上的解集不是空集的 的取值是
的取值是
A.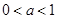 | B.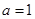 | C.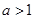 | D.以上均不对 |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.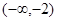 | B.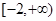 | C.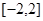 | D.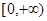 |
不等式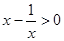 成立的充分不必要条件是( )
成立的充分不必要条件是( )
A.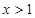 | B.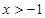 |
C.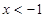 或 或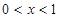 | D.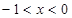 或 或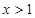 |
设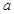 、
、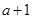 、
、 为钝角三角形的边,则
为钝角三角形的边,则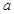 的取值范围是 ( )
的取值范围是 ( )
| A.0<a<3 | B.3<a<4 | C.1<a<3 | D.4<a<6 |
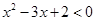 的解集为( )
的解集为( )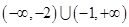 B.
B.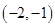
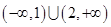 D.
D.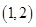
 :x
:x
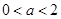
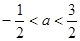

 的解集是_____ ___.
的解集是_____ ___.