题目内容
对数函数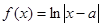 在
在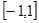 区间上恒有意义,则
区间上恒有意义,则 的取值范围是( )
的取值范围是( )
A.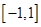 | B.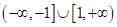 |
C.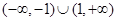 | D.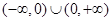 |
C
解析试题分析:由已知得 在
在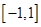 上恒成立,即
上恒成立,即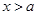 或
或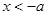 在
在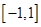 上恒成立,则只要
上恒成立,则只要 不在区间
不在区间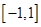 内即可,
内即可,
∴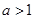 或
或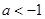 .
.
考点:绝对值不等式.

练习册系列答案
相关题目
不等式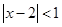 的解集为( )
的解集为( )
A.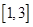 | B.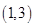 | C.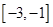 | D.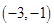 |
已知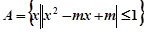 ,若
,若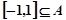 ,则实数
,则实数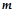 的取值范围为( )
的取值范围为( )
A. | B.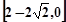 | C.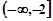 | D. |
设集合 ,
,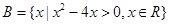 ,则
,则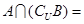 ( )
( )
A.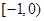 | B.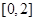 | C.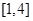 | D. |
不等式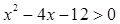 的解集是
的解集是
A.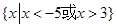 | B.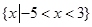 |
C.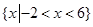 | D.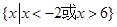 |
若不等式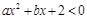 的解集为
的解集为 或
或 ,则
,则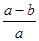 的值为( )
的值为( )
A. | B.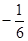 | C.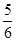 | D. |
若不等式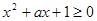 对任意
对任意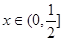 成立,则
成立,则 的最小值为( )
的最小值为( )
| A.0 | B.-2 | C.-3 | D.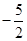 |
要证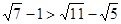 ,只需证
,只需证 ,即需
,即需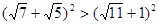 ,即需证
,即需证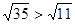 ,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
| A.比较法 | B.综合法 | C.分析法 | D.反证法 |
若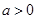 ,使不等式
,使不等式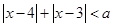 在
在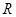 上的解集不是空集的
上的解集不是空集的 的取值是
的取值是
A.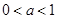 | B.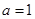 | C.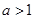 | D.以上均不对 |