题目内容
已知二次函数f(x)满足以下两个条件:①不等式f(x)<0的解集是(-2,0)
②函数f(x)在x∈[1,2]上的最小值是3
(Ⅰ)求f(x)的解析式;
(Ⅱ)若点(an,an+1)(n∈N*)在函数f(x)的图象上,且a1=99
(ⅰ)求证:数列{lg(1+an)}为等比数列
(ⅱ)令bn=lg(1+an),是否存在正实数k,使不等式kn2bn>(n+1)bn+1对于一切的n∈N*恒成立?若存在,指出k的取值范围;若不存在,请说明理由.
【答案】分析:(Ⅰ)由题意,设f(x)=ax(x+2)(a>0),确定函数的对称轴,利用函数f(x)在x∈[1,2]上的最小值,即可求得函数解析式;
(Ⅱ)(ⅰ)利用点(an,an+1)(n∈N*)在函数f(x)的图象上,化简可得lg(1+an+1)=2lg(1+an),即可证得数列{lg(1+an)}是以2为首项,2为公比的等比数列;
(ⅱ)要使不等式kn2bn>(n+1)bn+1对于一切的n∈N*恒成立,则kn2-2n-2>0对于一切的n∈N*恒成立.利用n=1时,k-2-2>0成立,可得k>4,再验证kn2-2n-2>0对于一切的n∈N*恒成立即可.
解答:(Ⅰ)解:由题意,设f(x)=ax(x+2)(a>0),∴函数的对称轴为直线x=-1
∴函数f(x)在x∈[1,2]上的最小值是f(1)=3a=3
∴a=1
∴f(x)的解析式为f(x)=ax(x+2);
(Ⅱ)(ⅰ)证明:∵点(an,an+1)(n∈N*)在函数f(x)的图象上,
∴an+1=an2+2an,∴1+an+1=(1+an)2,
∴lg(1+an+1)=2lg(1+an)
∵a1=99
∴lg(1+a1)=2
∴数列{lg(1+an)}是以2为首项,2为公比的等比数列;
(ⅱ)解:bn=lg(1+an)=2n,要使不等式kn2bn>(n+1)bn+1对于一切的n∈N*恒成立,则kn2-2n-2>0对于一切的n∈N*恒成立.
n=1时,k-2-2>0成立,即k>4;
设g(n)=kn2-2n-2,当k>4时,由于对称轴为n=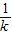 <1,且g(1)>0,而函数f(x)在[1,+∞)上是增函数
<1,且g(1)>0,而函数f(x)在[1,+∞)上是增函数
∴kn2-2n-2>0对于一切的n∈N*恒成立
∴k>4时,不等式kn2bn>(n+1)bn+1对于一切的n∈N*恒成立.
点评:本题考查函数的解析式,考查等比数列的证明,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.
(Ⅱ)(ⅰ)利用点(an,an+1)(n∈N*)在函数f(x)的图象上,化简可得lg(1+an+1)=2lg(1+an),即可证得数列{lg(1+an)}是以2为首项,2为公比的等比数列;
(ⅱ)要使不等式kn2bn>(n+1)bn+1对于一切的n∈N*恒成立,则kn2-2n-2>0对于一切的n∈N*恒成立.利用n=1时,k-2-2>0成立,可得k>4,再验证kn2-2n-2>0对于一切的n∈N*恒成立即可.
解答:(Ⅰ)解:由题意,设f(x)=ax(x+2)(a>0),∴函数的对称轴为直线x=-1
∴函数f(x)在x∈[1,2]上的最小值是f(1)=3a=3
∴a=1
∴f(x)的解析式为f(x)=ax(x+2);
(Ⅱ)(ⅰ)证明:∵点(an,an+1)(n∈N*)在函数f(x)的图象上,
∴an+1=an2+2an,∴1+an+1=(1+an)2,
∴lg(1+an+1)=2lg(1+an)
∵a1=99
∴lg(1+a1)=2
∴数列{lg(1+an)}是以2为首项,2为公比的等比数列;
(ⅱ)解:bn=lg(1+an)=2n,要使不等式kn2bn>(n+1)bn+1对于一切的n∈N*恒成立,则kn2-2n-2>0对于一切的n∈N*恒成立.
n=1时,k-2-2>0成立,即k>4;
设g(n)=kn2-2n-2,当k>4时,由于对称轴为n=
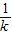 <1,且g(1)>0,而函数f(x)在[1,+∞)上是增函数
<1,且g(1)>0,而函数f(x)在[1,+∞)上是增函数∴kn2-2n-2>0对于一切的n∈N*恒成立
∴k>4时,不等式kn2bn>(n+1)bn+1对于一切的n∈N*恒成立.
点评:本题考查函数的解析式,考查等比数列的证明,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目