题目内容
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数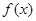 =
= .
.
(1)判断函数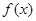 的奇偶性,并证明;
的奇偶性,并证明;
(2)求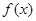 的反函数
的反函数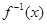 ,并求使得函数
,并求使得函数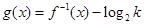 有零点的实数
有零点的实数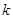 的取值范围.
的取值范围.
【答案】
(1)奇函数,用定义证明即可(2)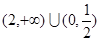
【解析】
试题分析:(1)由表达式可知f(x)的定义域为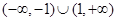 , ……2分
, ……2分
f(-x)=log2 =log2
=log2 =-f(x),
=-f(x),
所以,f(x)为奇函数. ……6分
(2)由y=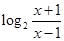 ,得x=
,得x= ,
,
所以,f -1(x)=
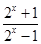 ,x
,x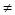 0. ……9分
0. ……9分
因为函数 有零点,
有零点,
所以,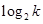 应在
应在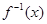 的值域内.
的值域内.
所以,log2k=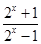 =1+
=1+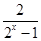
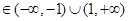 , ……13分
, ……13分
从而,k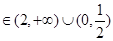 . ……14分
. ……14分
考点:本小题主要考查函数的奇偶性的判断和反函数的求解以及函数的值域问题,考查学生转化问题的能力和运算求解能力.
点评:无论考查函数的什么性质,都不要忘记先考查函数的定义域,而函数的奇偶性要求函数的定义域关于原点对称.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).