题目内容
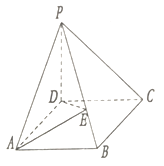
【题目】已知△ABC中，AC=1， 
，设∠BAC=x，记 
；
（1）求函数f（x）的解析式及定义域；
（2）试写出函数f（x）的单调递增区间，并求方程 
的解．
【答案】
（1）解：由正弦定理有 
= 
= 
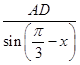
∴BC= sinx，AB= 
，
∴ 
= 
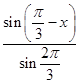sinxsin（ 
﹣x） 
= 
（ 
cosx﹣ sinx）sinx= 
sin（2x+ 
）﹣ 
，
其定义域为（0， ）
（2）解：∵﹣ 
+2kπ≤2x+ ≤ +2kπ，k∈Z，
∴﹣ +kπ≤x≤ +kπ，k∈Z，
∵x∈（0， ）
∴递增区间 
，
∵方程 
= sin（2x+ ）﹣ 
，
∴sin（2x+ ）=1，
解得 
．
【解析】（1）由条件利用正弦定理、两个向量的数量积公式、三角恒等变换化简函数f（x）的解析式．（2）利用正弦函数的单调性求得f（x）的单调区间，并求出x的值．
练习册系列答案
相关题目
