题目内容
【题目】点M（20，40），抛物线y2=2px（p＞0）的焦点为F，若对于抛物线上的任意点P，|PM|+|PF|的最小值为41，则p的值等于 ．
【答案】42或22
【解析】解：由抛物线的定义可知：抛物线上的点到焦点距离=到准线的距离， 过P做抛物线的准线的垂线，垂足为D，则|PF|=|PD|，
当M（20，40）位于抛物线内，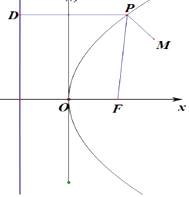
∴|PM|+|PF|=|PM|+|PD|，
当M，P，D共线时，|PM|+|PF|的距离最小，
由最小值为41，即20+ 
=41，解得：p=42，
当M（20，40）位于抛物线外，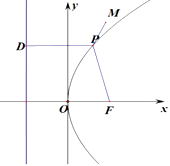
当P，M，F共线时，|PM|+|PF|取最小值，
即 
=41，解得：p=22或58，
由当p=58时，y2=116x，则点M（20，40）在抛物线内，舍去，
所以答案是：42或22．
练习册系列答案
发散思维新课堂系列答案
相关题目
