题目内容
【题目】已知数列 ![]() 满足
满足 ![]() ,
, ![]() ,求证:
,求证:
(I) ![]() ;
;
(II) ![]() ;
;
(III) ![]() .
.
【答案】解:(I)(数学归纳法)
当 ![]() 时,因为
时,因为 ![]() ,所以
,所以 ![]() 成立.
成立.
假设当 ![]() 时,
时, ![]() 成立,
成立,
则当 ![]() 时,
时, ![]() .
.
因为 ![]() ,
,
且 ![]() 得
得 ![]()
所以 ![]() 也成立.
也成立.
(II)因为 ![]() ,
,
所以 ![]()
所以 ![]() .
.
(III)因为 ![]() ,所以
,所以 ![]() .
.
从而 ![]() .
.
所以 ![]() ,即
,即 ![]() .
.
所以 ![]() .
.
又 ![]() ,故
,故 ![]() .
.
【解析】此题主要考查归纳法的证明,归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证,这是数列的通项一种常用求解的方法.
【考点精析】解答此题的关键在于理解数学归纳法的作用的相关知识,掌握用数学归纳法可以证明许多与自然数有关的数学命题,其中包括恒等式、不等式、数列通项公式、几何中的计算问题等,以及对数学归纳法的步骤的理解,了解
- 步骤:A.命题在n=1(或
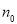 )时成立,这是递推的基础;B.假设在n=k时命题成立; C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=
)时成立,这是递推的基础;B.假设在n=k时命题成立; C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=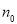 ,且
,且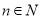 )结论都成立
)结论都成立
.

练习册系列答案
相关题目



