题目内容
【题目】已知函数 ![]() .
.
(1)求不等式 ![]() 的解集;
的解集;
(2)若关于 ![]() 的不等式
的不等式 ![]() 的解集不是空集,求实数
的解集不是空集,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:原不等式等价于 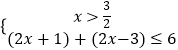 或
或 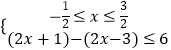
或  ,解得
,解得 ![]() 或
或 ![]() 或
或 ![]() .
.
∴原不等式的解集为 ![]()
(2)解: ![]() ,
,![]() 或
或 ![]() ,
,
∴实数 ![]() 的取值范围为
的取值范围为 ![]()
【解析】(1)根据题目中所给的条件的特点,通过分类讨论,去掉绝对值,求出不等式的解集;
(2)根据绝对值的性质求出f(x)的最小值,将原问题转化为解关于a的不等式,解出其解集即可得到答案.
|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法:
方法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想.
方法二:利用“零点分段法”求解,体现了分类讨论的思想;
方法三:通过构造函数,利用函数的图象求解,体现了函数与方程的思想.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目