题目内容
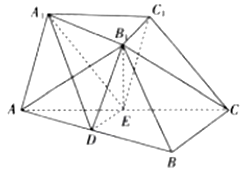
【题目】已知椭圆 
的左、右焦点分别为 
短轴两个端点为 
且四边形 
是边长为 
的正方形．
（Ⅰ）求椭圆的方程；
（Ⅱ）若 
分别是椭圆长轴的左、右端点，动点 
满足 
，连接 
，交椭圆于点 
．证明： 
为定值．
【答案】解：（I） 
， 
，∴ 
，
∴椭圆方程为 
．
（Ⅱ） 
， 
，设 
， 
，
则 
， 
，
直线 
，即 
，
代入椭圆 
得 
，
∵ 
，∴ 
， 
，
∴ 
，
∴ 
（定值）
【解析】（1）根据题目中所给的条件的特点，关键是利用椭圆的几何性质求出a、b的值，写出椭圆的标准方程即可．
（2）设出点M的坐标后写出直线CM的方程，并把它和椭圆的方程联立，解方程组可求P的坐标，进而得到向量OM、OP的坐标，计算它们的数量积，即可证明出定值．
练习册系列答案
相关题目
【题目】根据国家环保部新修订的《环境空气质量标准》规定：居民区 
的年平均浓度不得超过3S微克/立方米， 的24小时平均浓度不得超过75微克/立方米．某市环保局随机抽取了一居民区2016年20天 的24小时平均浓度（单位：微克/立方米）的监测数据，数据统计如图表：
组别 |
| 频数（天） | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
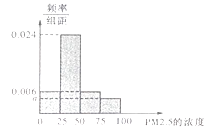
（Ⅰ）将这20天的测量结果按表中分组方法绘制成的样本频率分布直方图如图．
（ⅰ）求图中 
的值；
（ⅱ）在频率分布直方图中估算样本平均数，并根据样本估计总体的思想，从 的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由．
（Ⅱ）将频率视为概率，对于2016年的某3天，记这3天中该居民区 的24小时平均浓度符合环境空气质量标准的天数为 
，求 的分布列和数学期望．
