题目内容
【题目】已知函数![]()
(1)当![]() 时,求满足
时,求满足![]() 的
的![]() 的取值:
的取值:
(2)若函数![]() 是定义在
是定义在![]() 上的奇函数
上的奇函数
①存在![]() ,不等式
,不等式![]() 有解,求
有解,求![]() 的取值范围;
的取值范围;
②若函数![]() 满足
满足![]() ,若对任意
,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() ,(2)①
,(2)①![]() ,②6
,②6
【解析】分析:(1)根据![]()
![]() ,可将方程
,可将方程![]()
![]() 转化为一元二次方程:
转化为一元二次方程:![]() ,再根据指数函数范围可得
,再根据指数函数范围可得![]() ,解得
,解得![]() ,(2)①先根据函数奇偶性确定
,(2)①先根据函数奇偶性确定![]() 值:
值:![]() ,再利用单调性定义确定其单调性;在
,再利用单调性定义确定其单调性;在![]() 上递调,最后根据单调性转化不等式
上递调,最后根据单调性转化不等式![]() 为
为![]() ,即
,即![]() 在
在![]() 时有解,根据判别式大于零可得
时有解,根据判别式大于零可得![]() 的取值范围。②先求函数
的取值范围。②先求函数![]() :
:![]() ,则
,则![]() ,因此不等式可转化为一元二次不等式,并将其变量分离得:
,因此不等式可转化为一元二次不等式,并将其变量分离得:![]() 的最小值,其中
的最小值,其中![]() ,利用基本不等式求最值得
,利用基本不等式求最值得![]()
详解:(1)由题意,![]() ,化简得
,化简得![]()
解得![]() (舍)或
(舍)或![]() ,
,
所以![]()
(2)因为![]() 是奇函数,所以
是奇函数,所以![]() ,所以
,所以![]()
化简并变形得:![]()
要使上式对任意![]() 的成立,则
的成立,则![]() 或
或![]()
解得:![]() 或
或![]() ,因为
,因为![]() 的定义域是
的定义域是![]() ,所以
,所以![]() 舍去
舍去
所以![]() ,所以
,所以![]()
①![]()
对任意![]() ,
,![]() 有:
有:
![]()
![]()
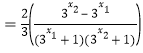
因为![]() ,所以
,所以![]() ,所以
,所以![]()
因此![]() 在
在![]() 上递减
上递减
因为![]() ,所以
,所以![]()
即![]() 在
在![]() 时有解,所以
时有解,所以![]() ,解得
,解得![]()
所以![]() 的取值范围为
的取值范围为![]()
②因为![]() ,所以
,所以![]()
即![]()
所以![]()
不等式![]() 恒成立,
恒成立,
即![]()
即![]() 恒成立,
恒成立,
令![]() ,
,![]() ,则
,则![]() 在
在![]() 时恒成立
时恒成立
令![]() ,
,![]()
![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减
上单调递减
![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
所以![]() ,所以
,所以![]()
所以,实数![]() 的最大值是6.
的最大值是6.

练习册系列答案
相关题目
【题目】某舆情机构为了解人们对某事件的关注度,随机抽取了![]() 人进行调查,其中女性中对该事件关注的占
人进行调查,其中女性中对该事件关注的占![]() ,而男性有
,而男性有![]() 人表示对该事件没有关注.
人表示对该事件没有关注.
关注 | 没关注 | 合计 | |
男 |
| ||
女 | |||
合计 |
(1)根据以上数据补全![]() 列联表;
列联表;
(2)能否有![]() 的把握认为“对事件是否关注与性别有关”?
的把握认为“对事件是否关注与性别有关”?
(3)已知在被调查的女性中有![]() 名大学生,这其中有
名大学生,这其中有![]() 名对此事关注.现在从这
名对此事关注.现在从这![]() 名女大学生中随机抽取
名女大学生中随机抽取![]() 人,求至少有
人,求至少有![]() 人对此事关注的概率.
人对此事关注的概率.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
![]()


