题目内容
9.设f(x)=aex+$\frac{1}{{a{e^x}}}$+b(a>0)( I) 设曲线y=f(x)在点(2,f(2))的切线方程为y=$\frac{3}{2}$x;求a,b的值.
( II)求f(x)在[0,+∞)上的最小值.
分析 (Ⅰ)由求导公式和法则求出f′(x),根据导数的几何意义和条件列出方程组,求出a、b的值;
(Ⅱ)设t=ex(t≥1),代入原函数化简并求出导数,根据临界点和区间对a进行分类讨论,利用导数与单调性、基本不等式求出函数的最小值.
解答 解:(I)由题意得,$f(x)=a{e}^{x}+\frac{1}{a{e}^{x}}+b$,则$f′(x)=a{e}^{x}-\frac{1}{a{e}^{x}}$,
因为在点(2,f(2))的切线方程为y=$\frac{3}{2}$x,所以$\left\{\begin{array}{l}{f(2)=3}\\{f′(2)=\frac{3}{2}}\end{array}\right.$,
即$\left\{\begin{array}{l}{a{e}^{2}+\frac{1}{a{e}^{2}}+b=3}\\{a{e}^{2}-\frac{1}{a{e}^{2}}=\frac{3}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{2}{{e}^{2}}}\\{b=\frac{1}{2}}\end{array}\right.$…(6分)
(Ⅱ)设t=ex(t≥1),则原函数化为:$y=at+\frac{1}{at}+b$,
所以$y′=a-\frac{1}{a{t}^{2}}$=$\frac{{a}^{2}{t}^{2}-1}{a{t}^{2}}$,
令y′=0,解得t=$±\frac{1}{a}$,
(1)当a≥1时,则y′>0在[1,+∞)上成立,
所以函数$y=at+\frac{1}{at}+b$在[1,+∞)上是增函数,
则当t=1(x=0)时,函数f(x)取到最小值是$a+\frac{1}{a}+b$;
(2)当0<a<1时,$y=at+\frac{1}{at}+b$≥2+b,
当且仅当at=1(t=ex=$\frac{1}{a}$>1,则x=-lna)时,取等号,
此时函数f(x)取到最小值是b+2,
综上可得,当a≥1时,函数f(x)的最小值是$a+\frac{1}{a}+b$;
当0<a<1时,函数f(x)的最小值是b+2.…(12分)
点评 本题考查求导公式和法则,导数的几何意义,以及导数与函数单调性、基本不等式求函数的最值问题,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
| A. | y=-2x | B. | y=3x | C. | y=-3x | D. | y=4x |
| A. | 等于 | B. | 小于 | C. | 大于 | D. | 不能确定 |
 在
在 上的导函数为
上的导函数为 ,若
,若 恒成立,且
恒成立,且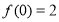 ,则不等式
,则不等式 的解集是( )
的解集是( ) B.
B.
 D.
D.
 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,侧面
,侧面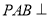 底面
底面 ,
,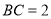 .
.
 平面
平面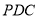 ;
;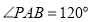 ,求点
,求点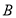 到直线
到直线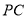 的距离.
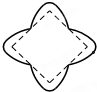
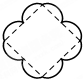
的距离. 如图:一个周长为1的圆沿着边长为2的正方形的边按逆时针方向滚动(无滑动),P是圆上的一定点,开始时PA⊥AB,当圆滚过正方形一周,回到起点时,点P所绘出的图形大致是( )
如图:一个周长为1的圆沿着边长为2的正方形的边按逆时针方向滚动(无滑动),P是圆上的一定点,开始时PA⊥AB,当圆滚过正方形一周,回到起点时,点P所绘出的图形大致是( )