题目内容
4.已知函数f(x)=mx-lnx(m∈R)(Ⅰ)当m=1时,求曲线y=f(x)在x=2处切线方程;
(Ⅱ)求f(x)的单调区间.
分析 (Ⅰ)先将m=1代入函数的表达式,求出函数的导数,从而求出切点的坐标以及直线的斜率,代入点斜式方程整理即可;
(Ⅱ)先求出函数的导数,通过讨论m的符号,从而得到函数的单调区间.
解答 解:(Ⅰ)m=1时,f(x)=x-lnx,
∴f′(x)=1-$\frac{1}{x}$,f′(2)=$\frac{1}{2}$,f(2)=2-ln2,
∴切线方程为:y-2+ln2=$\frac{1}{2}$(x-2),
即:x-2y-2ln2+2=0.
(Ⅱ)∵f′(x)=m-$\frac{1}{x}$=$\frac{mx-1}{x}$,(x>0),
①m>0时,令f′(x)>0,解得:x>$\frac{1}{m}$,
令f′(x)<0,解得:0<x<$\frac{1}{m}$,
∴f(x)在(0,$\frac{1}{m}$)递减,在($\frac{1}{m}$,+∞)递增,
②m<00时,f′(x)<0,
∴f(x)在(0,+∞)递减.
点评 本题考查了函数的单调性,导数的应用,考查曲线的切线方程问题,是一道中档题.

练习册系列答案
相关题目
13.已知PC为球O的直径,A,B是球面上两点,且AB=6,∠APC=∠BPC=$\frac{π}{4}$若球O的表面积为64π,则棱锥A-PBC的体积为( )
| A. | $8\sqrt{7}$ | B. | $24\sqrt{7}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{21}}}{5}$ |
12.函数y=cosx的单调减区间为(k∈Z)( )
| A. | [-π+2kπ,π+2kπ] | B. | [-$\frac{π}{2}$π+2kπ,$\frac{3}{2}$π+2kπ] | ||
| C. | [π+2kπ,2π+2kπ] | D. | [2kπ,π+2kπ] |
 上的函数
上的函数 是偶函数,且
是偶函数,且 时,
时, .
. 时,求
时,求 解析式;
解析式; 的单调递增区间.
的单调递增区间. .
. 时,求不等式
时,求不等式 的解集;
的解集; 的图象与
的图象与 轴围成的三角形面积大于6,求
轴围成的三角形面积大于6,求 的取值范围.
的取值范围. ,下列命题正确的是 .
,下列命题正确的是 . 关于原点
关于原点 中心对称;
中心对称; ,
, 两不同的点为切点作两条互相平行的切线,分别与
两不同的点为切点作两条互相平行的切线,分别与 交于
交于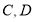 两点,则这四个点的横坐标满足关系
两点,则这四个点的横坐标满足关系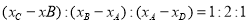 ;
; 为切点,作切线与
为切点,作切线与 ,再以点
,再以点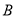 为切点作直线与
为切点作直线与 ,再以点
,再以点 作切点作直线与
作切点作直线与 ,则
,则 点横坐标为
点横坐标为 ;
; ,函数
,函数 ,使得以它们为顶点的四边形有且仅有一个正方形.
,使得以它们为顶点的四边形有且仅有一个正方形.