Question

【题目】如图，在三棱锥S﹣ABC中，SA=SC，AB⊥AC，D为BC的中点，E为AC上一点，且DE∥平面SAB．求证：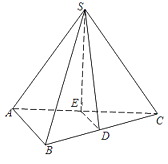

（1）直线AB∥平面SDE；
（2）平面ABC⊥平面SDE．

Answer 1

【答案】
（1）证明：因为DE∥平面SAB，DE平面ABC，平面SAB∩平面ABC=AB，

所以DE∥AB，

因为DE平面SDE，AB平面SDE，

所以AB∥平面SDE

（2）证明：因为D为BC的中点，DE∥AB，

所以E为AC的中点．

又因为SA=SC，所以SE⊥AC，

又AB⊥AC，DE∥AB，

所以DE⊥AC，

∵DE平面SDE，SE平面SDE，DE∩SE=E，

所以AC⊥平面SDE，

因为AC平面ABC，

所以平面ABC⊥平面SDE

【解析】（1）由线面平行的性质定理可得出DE∥AB，再由线面平行的判定定理得到线面平行。（2）由已知可得SE⊥AC，再利用平行的传递性可得DE⊥AC，由线面垂直的判定定理可得AC⊥平面SDE，，进而得到面面垂直。
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．