题目内容
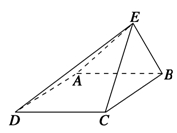
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB//CD,AB=AD=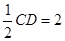 ,点M在线段EC上且不与E、C垂合.
,点M在线段EC上且不与E、C垂合.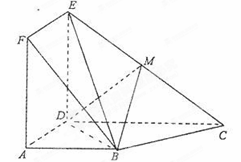
(1)当点M是EC中点时,求证:BM//平面ADEF;
(2)当平面BDM与平面ABF所成锐二面角的余弦值为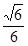 时,求三棱锥M—BDE的体积.
时,求三棱锥M—BDE的体积.
(1)详见解析;(2)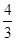 .
.
解析试题分析:(1)建立空间直角坐标系,由题意计算平面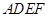 的法向量,由法向量与向量
的法向量,由法向量与向量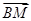 垂直,从而证明了BM//平面ADEF;(2)设出
垂直,从而证明了BM//平面ADEF;(2)设出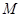 点的坐标,由平面BDM与平面ABF所成锐二面角的余弦值为
点的坐标,由平面BDM与平面ABF所成锐二面角的余弦值为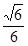 ,分别计算两个半平面的法向量,代入夹角公式,从而得到
,分别计算两个半平面的法向量,代入夹角公式,从而得到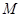 点.三棱锥M—BDE中由于
点.三棱锥M—BDE中由于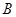 到面
到面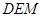 的距离容易得知,故以
的距离容易得知,故以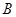 为顶点,再计算出底面三角形
为顶点,再计算出底面三角形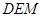 ,利用棱锥的体积公式即可得到所求.
,利用棱锥的体积公式即可得到所求.
试题解析:(1)以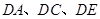 分别为
分别为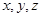 轴建立空间直角坐标系
轴建立空间直角坐标系
则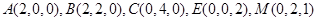
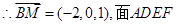 的一个法向量
的一个法向量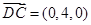
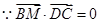 ,
,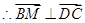 .即
.即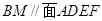 4分
4分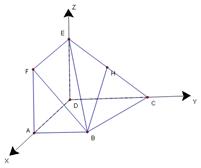
(2)依题意设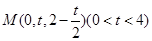 ,设面
,设面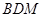 的法向量
的法向量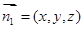
则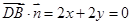 ,
,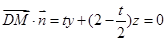
令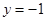 ,则
,则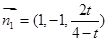 ,面
,面 的法向量
的法向量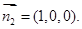
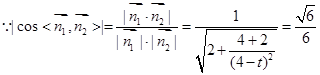 ,解得
,解得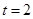
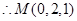 为EC的中点,
为EC的中点,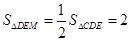 ,
,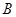 到面
到面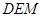 的距离
的距离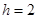
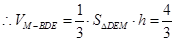 12分
12分
考点:1.线面平行的判定;2.二面角;3.三棱锥的体积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
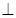 底面ABCD,且SA=2,AD=DC=1
底面ABCD,且SA=2,AD=DC=1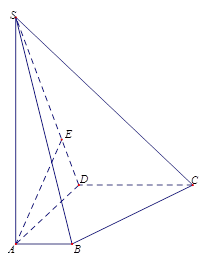
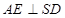 证明:
证明: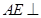 平面
平面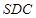 ;
;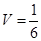 ,求面SAD与面SBC所成二面角的正弦值的大小
,求面SAD与面SBC所成二面角的正弦值的大小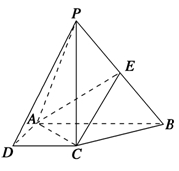
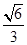 ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.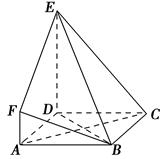
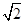 .
.
 为直角梯形,
为直角梯形, ,
, ,
,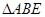 为等边三角形,且平面
为等边三角形,且平面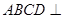 平面
平面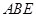 ,
,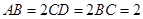 ,
,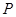 为
为 中点.
中点.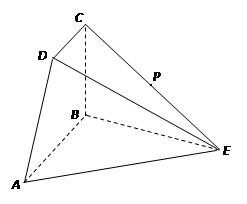
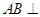
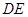 ;
;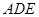 与平面
与平面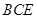 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;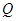 ,使
,使 平面
平面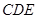 ,如果存在,求
,如果存在,求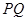 的长;如果不存在,说明理由.
的长;如果不存在,说明理由.  中,M,N分别是线段
中,M,N分别是线段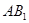 和BD上的点,且AM=BN=
和BD上的点,且AM=BN=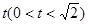
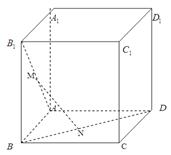
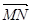 |的最小值;
|的最小值; 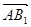 ,
,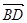 是否都垂直,如果都垂直给出证明;如果不是都垂直,说明理由.
是否都垂直,如果都垂直给出证明;如果不是都垂直,说明理由.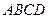 是边长为
是边长为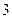 的正方形,
的正方形,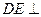 平面
平面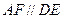 ,
, ,
, 与平面
与平面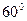

 点
点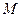 是线段
是线段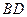 上一个动点,试确定点
上一个动点,试确定点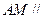 平面
平面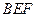 ,并证明你的结论 ;
,并证明你的结论 ; 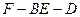 的余弦值
的余弦值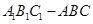 中,
中,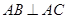 ,
,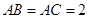 ,
,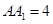 ,点
,点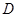 是
是 的中点.
的中点.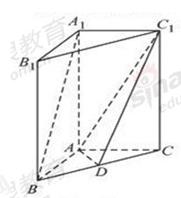
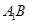 与
与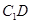 所成角的余弦值;
所成角的余弦值;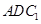 与平面
与平面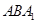 所成二面角的正弦值.
所成二面角的正弦值.