题目内容
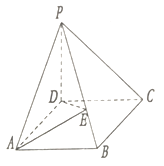
【题目】如图,在正四棱锥P﹣ABCD中,PA=AB=a,E是棱PC的中点. 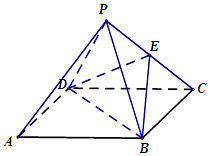
(1)求证:PC⊥BD;
(2)求直线BE与PA所成角的余弦值.
【答案】
(1)证明:∵四边形ABCD为正方形,且PA=AB=a,
∴△PBC,△PDC都是等边三角形,
∵E是棱PC的中点,
∴BE⊥PC,DE⊥PC,又 BE∩DE=E,
∴PC⊥平面BDE
又BD平面BDE,
∴PC⊥BD
(2)解:连接AC,交BD于点O,连OE.
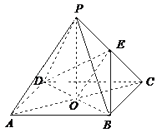
四边形ABCD为正方形,∴O是AC的中点
又E是PC的中点
∴OE为△ACP的中位线,∴AP∥OE
∴∠BOE即为BE与PA所成的角
在Rt△BOE中,BE= ![]() ,EO=
,EO= ![]() ,
,
∴ ![]() .
.
∴直线BE与PA所成角的余弦值为 ![]() .
.
【解析】(1)推导出△PBC,△PDC都是等边三角形,从而BE⊥PC,DE⊥PC,由此能证明PC⊥BD.(2)连接AC,交BD于点O,连OE,则AP∥OE,∠BOE即为BE与PA所成的角,由此能求出直线BE与PA所成角的余弦值.
【考点精析】掌握异面直线及其所成的角和直线与平面垂直的性质是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;垂直于同一个平面的两条直线平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目