Question

椭圆

x2

9

+

y2

4

=1的右焦点为F，P₁，P₂，…，P₂₄为24个依逆时针顺序排列在椭圆上的点，其中P₁是椭圆的右顶点，并且∠P₁FP₂=∠P₂FP₃=∠P₃FP₄=…=∠P₂₄FP₁．若这24个点到右准线的距离的倒数和为S，求S²的值．

Answer 1

分析：由椭圆的方程得到相应a，b，c的值，若设|FP|=r，P到准线的距离|PH|=d，FP与X轴正方向的夹角为θ，则得到

1

d

=

c

b2

（1+ecosθ），求和后，即可得到S²的值．

解答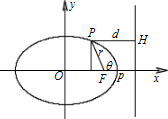：解：由于椭圆的方程为

x2

9

+

y2

4

=1，则a=3，b=2，c=

5

，

b2

c

=

4

5

，
对于椭圆上任一点P，|FP|=r，P到准线的距离|PH|=d，FP与X轴正方向的夹角为θ，则有
rcosθ+d=

b2

c

，

r

d

=e．
于是，d（1+ecosθ）=

b2

c

，则

1

d

=

c

b2

（1+ecosθ）
所以S=

24

i=1

1

di

=

c

b2

24

i=1

（1+ecosθ）=

c

b2

+

c

b2

×e

24

i=1

cosθ=

c

b2

故S²=（

c

b2

）²=(

24× 5

4

)2=180．

点评：本题考查椭圆的性质，注意转化与化归思想的应用．