题目内容
设P(x,y)为椭圆
+
=1上的动点,A(a,0)(0<a<3)为定点,已知|AP|的最小值为1,求a的值.
| x2 |
| 9 |
| y2 |
| 4 |
分析:由P(x,y)为椭圆
+
=1上的动点,A(a,0)(0<a<3)为定点,知|AP|2=(x-a)2+y2=(x-a)2+4-
x2=
(x-
)2+4-
,x∈[-3,3]及|AP|的最小值为1,能求出a的值.
| x2 |
| 9 |
| y2 |
| 4 |
| 4 |
| 9 |
| 5 |
| 9 |
| 9a |
| 5 |
| 4a2 |
| 5 |
解答:解:∵P(x,y)为椭圆
+
=1上的动点,A(a,0)(0<a<3)为定点,
∴|AP|2=(x-a)2+y2=(x-a)2+4-
x2
=
(x-
)2+4-
,x∈[-3,3],
∵0<a<3,∴0<
<
,
当0<
≤3,即0<a≤
时,
|AP|2min=4-
a2=1,解得a=
(舍);
当
>3,即3>a>
时,
当x=3时取最小值,
则|AP|2min=a2-6a+9=1,解得a=2,或a=4(舍).
综上,a=2
| x2 |
| 9 |
| y2 |
| 4 |
∴|AP|2=(x-a)2+y2=(x-a)2+4-
| 4 |
| 9 |
=
| 5 |
| 9 |
| 9a |
| 5 |
| 4a2 |
| 5 |
∵0<a<3,∴0<
| 9a |
| 5 |
| 27 |
| 5 |
当0<
| 9a |
| 5 |
| 5 |
| 3 |
|AP|2min=4-
| 4 |
| 5 |
| ||
| 2 |
当
| 9a |
| 5 |
| 5 |
| 3 |
当x=3时取最小值,
则|AP|2min=a2-6a+9=1,解得a=2,或a=4(舍).
综上,a=2
点评:本题考查满足条件的实数值的求法,具体涉及到椭圆的性质,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
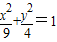 上的动点,A(a,0)(0<a<3)为定点,已知|AP|的最小值为1,求a的值.
上的动点,A(a,0)(0<a<3)为定点,已知|AP|的最小值为1,求a的值.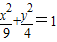 上的动点,A(a,0)(0<a<3)为定点,已知|AP|的最小值为1,求a的值.
上的动点,A(a,0)(0<a<3)为定点,已知|AP|的最小值为1,求a的值.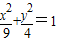 上的动点,A(a,0)(0<a<3)为定点,已知|AP|的最小值为1,求a的值.
上的动点,A(a,0)(0<a<3)为定点,已知|AP|的最小值为1,求a的值.