Question

已知实数x、y满足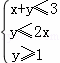，则z=x﹣3y的最大值为（　　）

A．

1

B．

﹣5

C．

﹣1

D．

﹣3

Answer 1

考点：

简单线性规划．

专题：

不等式的解法及应用．

分析：

画出满足条件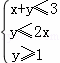的可行域，求出各角点的坐标，分别代入目标函数的解析式，求出目标函数的值，比较后，可得目标函数的最大值．

解答：

解：满足条件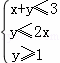的可行域如下图所示：

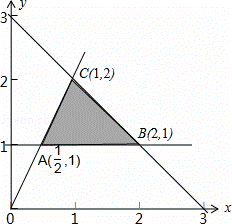
∵z=x﹣3y

∴z_A=，z_B=﹣1，z_A=﹣5，

故z=x﹣3y的最大值为﹣1

故选C

点评：

本题考查的知识点是简单线性规划，线性规划是高考的必考内容，“角点法”是解答此类问题最常用的方法，一定要熟练掌握．