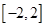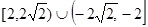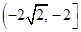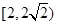题目内容
已知直线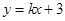 与圆
与圆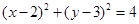 相交于
相交于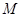 ,
,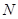 两点,若
两点,若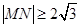 ,则
,则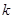 的取值范围为( )
的取值范围为( )
A.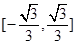 | B. |
C.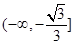 | D.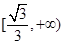 |
A
解析试题分析:由圆的方程可知圆心为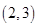 ,半径为2。圆心到直线
,半径为2。圆心到直线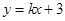 的距离
的距离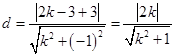 。因为
。因为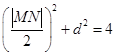 ,所以
,所以 ,因为
,因为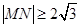 ,所以
,所以 ,解得
,解得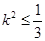 ,所以
,所以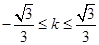 。故A正确。
。故A正确。
考点:1点到直线的距离;2直线和圆的相交弦问题。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
动圆C经过点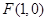 ,并且与直线
,并且与直线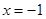 相切,若动圆C与直线
相切,若动圆C与直线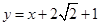 总有公共点,则圆C的面积( )
总有公共点,则圆C的面积( )
A.有最大值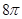 | B.有最小值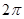 | C.有最小值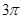 | D.有最小值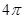 |
圆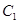 :
: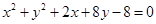 与圆
与圆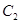 :
: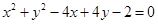 的位置关系是( )
的位置关系是( )
| A.相交 | B.外切 | C.内切 | D.相离 |
圆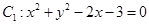 与圆
与圆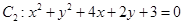 的位置关系为 ( )
的位置关系为 ( )
| A.两圆相交 | B.两圆相外切 | C.两圆相内切 | D.两圆相离 |
已知圆的方程为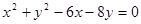 ,过点
,过点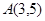 的直线被圆所截,则截得的最短弦的长度为 ( ).
的直线被圆所截,则截得的最短弦的长度为 ( ).
A.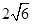 | B.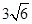 | C.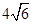 | D.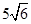 |
过圆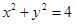 上的一点
上的一点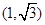 的圆的切线方程是 ( )
的圆的切线方程是 ( )
A.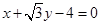 | B.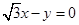 |
C.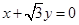 | D.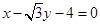 |
过点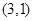 作圆
作圆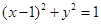 的两条切线,切点分别为
的两条切线,切点分别为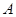 ,
,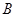 ,则直线
,则直线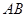 的方程为( )
的方程为( )
A. | B.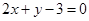 | C.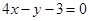 | D.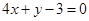 |
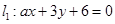 ,
,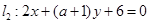 ,和圆C:
,和圆C: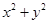
 的位置关系是“平行相交”,则b的取值范围为( )
的位置关系是“平行相交”,则b的取值范围为( )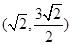
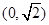
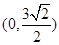

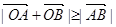 ,则实数
,则实数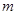 的取值范围是( )
的取值范围是( )