题目内容
9.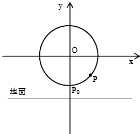 如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为8cm,圆环的圆心O距离地面的高度为10m,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点P0处
如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为8cm,圆环的圆心O距离地面的高度为10m,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点P0处(1)试确定在时刻t(min)时蚂蚁距离地面的高度h(m)
(2)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过14m?
分析 (1)先算出以OP为终边的角,根据三角函数求解;
(2)利用三角函数的性质进行求解.
解答 解:(1)设在时刻t(min)时蚂蚁达到点P,由OP在t分钟内所转过的角为$\frac{2π}{12}t$=$\frac{π}{6}t$,
可知以Ox为始边,OP为终边的角为$\frac{π}{6}t$+$\frac{3}{2}π$,
则P点的纵坐标为8sin($\frac{π}{6}t$+$\frac{3}{2}π$),
则h=8sin($\frac{π}{6}t$+$\frac{3}{2}π$)+10=10-8cos$\frac{π}{6}t$,
∴h=10-8cos$\frac{π}{6}t$(t≥0)
(2)h=10-8cos$\frac{π}{6}t$≥14⇒cos$\frac{π}{6}t$≤-$\frac{1}{2}$
⇒$\frac{2}{3}π+2kπ≤$$\frac{π}{6}t$$≤\frac{4}{3}π+2kπ$(k∈Z)
因为所研究的问题在蚂蚁绕圆环爬行的一圈内,故不妨令t∈[0,12],
∴4≤t≤8
所以在蚂蚁绕圆环爬行的一圈内,有4分钟时间蚂蚁距离地面超过14m.
故答案为:(1)h=10-8cos$\frac{π}{6}t$(t≥0)
(2)4分钟.
点评 本题考查了在实际问题中学生建立三角函数模型的能力.

练习册系列答案
相关题目
15.若f(x)为奇函数,且x0是y=f(x)-ex的一个零点,则-x0一定是下列哪个函数的零点( )
| A. | y=f(x)ex+1 | B. | y=f(-x)e-x-1 | C. | y=f(x)ex-1 | D. | y=f(-x)ex+1 |
16.在等差数列{an}中,已知a18=3(4-a2),则该数列的前11项和S11等于( )
| A. | 33 | B. | 44 | C. | 55 | D. | 66 |
 在三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥AC.D,E分别是BB1,A1C1的中点.
在三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥AC.D,E分别是BB1,A1C1的中点. 某校对学生的上学时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,若用分层抽样的方法从该校400名学生中抽取一个容量为20的样本,设m,n表示某两名学生的上学所需时间,且已知m,n∈[40,60)∪[80,100],则事件|m-n|<20的概率为$\frac{2}{5}$.
某校对学生的上学时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,若用分层抽样的方法从该校400名学生中抽取一个容量为20的样本,设m,n表示某两名学生的上学所需时间,且已知m,n∈[40,60)∪[80,100],则事件|m-n|<20的概率为$\frac{2}{5}$. 如图所示,△ABC内接于⊙O,PA是⊙O的切线,PB⊥PA,BE=PE=2PD=4,则PA=4,AC=5$\sqrt{2}$.
如图所示,△ABC内接于⊙O,PA是⊙O的切线,PB⊥PA,BE=PE=2PD=4,则PA=4,AC=5$\sqrt{2}$.