题目内容
【题目】设![]() 是圆
是圆![]() 上的一动点,点
上的一动点,点![]() 在直线
在直线![]() 上线段
上线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() .
.
(1)若点![]() 的轨迹为椭圆,则求
的轨迹为椭圆,则求![]() 的取值范围;
的取值范围;
(2)设![]() 时对应的椭圆为
时对应的椭圆为![]() ,
,![]() 为椭圆的右顶点,直线
为椭圆的右顶点,直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由已知可得点![]() 在
在![]() 的垂直平分线上,有
的垂直平分线上,有![]() ,进而
,进而![]() ,根据点
,根据点![]() 的轨迹为椭圆,由椭圆定义可得
的轨迹为椭圆,由椭圆定义可得![]() ,即
,即![]() 在圆
在圆![]() 外,得出
外,得出![]() 不等量关系,结合
不等量关系,结合![]() 关系,即可求解;
关系,即可求解;
(2)根据(1)求出椭圆方程,设出直线![]() ,以及
,以及![]() ,
,![]() ,根据直线与椭圆相交关系结合韦达定理,求出
,根据直线与椭圆相交关系结合韦达定理,求出![]() 的值,
的值,![]() 转坐标关系,可得出直线
转坐标关系,可得出直线![]() 过定点
过定点![]() ,得到
,得到![]() ,再利用韦达定理,求出
,再利用韦达定理,求出![]() 关于
关于![]() 的目标函数,结合
的目标函数,结合![]() 的范围,利用换元法,转化为二次函数的最值,即可求解.
的范围,利用换元法,转化为二次函数的最值,即可求解.
解:(1)若![]() 的轨迹为椭圆,则
的轨迹为椭圆,则![]() 必在圆内,
必在圆内,
此时![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() 在直线
在直线![]() 上,∴
上,∴![]() ,
,
∴![]() ,则
,则![]() .
.
(2)当![]() 时,
时,![]() 为
为![]() ,此时
,此时![]() ,
,
∴![]() 的轨迹为以
的轨迹为以![]() 、
、![]() 为焦点的椭圆,其中
为焦点的椭圆,其中![]() ,
,![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
∵![]() 为右顶点,∴
为右顶点,∴![]() 为
为![]() ,设
,设![]() ,
,![]() ,
,
![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
即![]() ,①
,①
∵![]() ,
,![]() 在直线
在直线![]() 上,
上,
∴①式变为![]() ,②
,②
联立直线方程与椭圆方程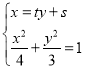 ,
,
得![]() ,
,
∴![]() ,
,![]() ,
,
代入②式得![]() ,∴
,∴![]() 或
或![]() ,
,
当![]() 时,
时,![]() 、
、![]() 或
或![]() 、
、![]() 重合,
重合,
与![]() 、
、![]() 为非零向量矛盾,舍去.
为非零向量矛盾,舍去.
∴![]() ,直线
,直线![]() 为
为![]() ,过定点
,过定点![]() ,
,
此时![]()
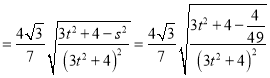
令![]() ,则
,则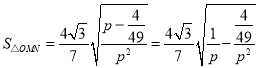 ,
,
∵![]() ,∴
,∴![]() ,
,
即![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目