题目内容
【题目】 (2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )

A.BE∥平面PAD,且BE到平面PAD的距离为![]()
B.BE∥平面PAD,且BE到平面PAD的距离为![]()
C.BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D.BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
【答案】D
【解析】

连接AC,BD,交点为O,连接OP,以O为坐标原点,OC,OD,OP所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系,由正四棱锥P-ABCD的棱长均为2,点E为PC的中点,知A(-![]() ,0,0),B(0,-
,0,0),B(0,-![]() ,0),C(
,0),C(![]() ,0,0),D(0,
,0,0),D(0,![]() ,0),P(0,0,
,0),P(0,0,![]() ),E
),E![]() ,则
,则![]() =
=![]() ,
,![]() =(-
=(-![]() ,0,-
,0,-![]() ),
),![]() =(0,
=(0,![]() ,-
,-![]() ),设m=(x,y,z)是平面PAD的法向量,则m⊥
),设m=(x,y,z)是平面PAD的法向量,则m⊥![]() ,且m⊥
,且m⊥![]() ,即
,即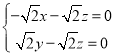 ,令x=1,则z=-1,y=-1,m=(1,-1,-1)是平面PAD的一个法向量,设BE与平面PAD所成的角为θ,则sinθ=
,令x=1,则z=-1,y=-1,m=(1,-1,-1)是平面PAD的一个法向量,设BE与平面PAD所成的角为θ,则sinθ=![]() ,故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°,故选D.
,故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°,故选D.

【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(Ⅲ)求![]() 关于
关于![]() 的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过
的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过![]() 万元.
万元.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
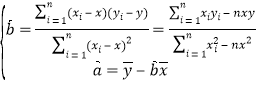
【题目】某大学高等数学这学期分别用![]() 两种不同的数学方式试验甲、乙两个大一新班(人数均为
两种不同的数学方式试验甲、乙两个大一新班(人数均为![]() 人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各
人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各![]() 名的高等数学期末考试成绩,得到茎叶图:
名的高等数学期末考试成绩,得到茎叶图:


(1)学校规定:成绩不得低于85分的为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
列联表,并判断“能否在犯错误率的概率不超过0.025的前提下认为成绩优异与教学方式有关?”
下面临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考方式:![]() ,其中
,其中![]() )
)
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率.
【题目】下表是某地一家超市在2018年一月份某一周内周2到周6的时间![]() 与每天获得的利润
与每天获得的利润![]() (单位:万元)的有关数据.
(单位:万元)的有关数据.
星期 | 星期2 | 星期3 | 星期4 | 星期5 | 星期6 |
利润 | 2 | 3 | 5 | 6 | 9 |
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(2)估计星期日获得的利润为多少万元.
参考公式: 