题目内容
（2013•东城区二模）如图，△BCD是等边三角形，AB=AD，∠BAD=90°，M，N，G分别是BD，BC，AB的中点，将△BCD沿BD折叠到△BC′D的位置，使得AD⊥C′B．（1）求证：平面GNM∥平面ADC′；
（2）求证：C′A⊥平面ABD．
分析：（1）利用线面平行的判定定理，证明MN∥平面ADC′，NG∥平面ADC，再利用面面平行的判定定理证明平面GNM∥平面ADC′；
（2）利用AD⊥平面C′AB，证明AD⊥C′A，利用勾股定理的逆定理，证明AB⊥C′A，再利用线面垂直的判定定理证明C′A⊥平面ABD．
（2）利用AD⊥平面C′AB，证明AD⊥C′A，利用勾股定理的逆定理，证明AB⊥C′A，再利用线面垂直的判定定理证明C′A⊥平面ABD．
解答：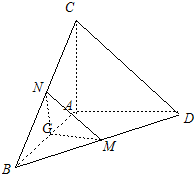
证明：（1）因为M，N分别是BD，BC′的中点，
所以MN∥DC′．
因为MN?平面ADC′，DC′?平面ADC′，
所以MN∥平面ADC′．
同理NG∥平面ADC′．
又因为MN∩NG=N，
所以平面GNM∥平面ADC′．
（2）因为∠BAD=90°，所以AD⊥AB．
又因为AD⊥C′B，且AB∩C′B=B，
所以AD⊥平面C′AB．
因为C′A?平面C′AB，所以AD⊥C′A．
因为△BCD是等边三角形，AB=AD，
不防设AB=1，则 BC=CD=BD=
，可得C′A=1．
由勾股定理的逆定理，可得AB⊥C′A．
因为AB∩AD=A，所以C′A⊥平面ABD． …（14分）
证明：（1）因为M，N分别是BD，BC′的中点，所以MN∥DC′．
因为MN?平面ADC′，DC′?平面ADC′，
所以MN∥平面ADC′．
同理NG∥平面ADC′．
又因为MN∩NG=N，
所以平面GNM∥平面ADC′．
（2）因为∠BAD=90°，所以AD⊥AB．
又因为AD⊥C′B，且AB∩C′B=B，
所以AD⊥平面C′AB．
因为C′A?平面C′AB，所以AD⊥C′A．
因为△BCD是等边三角形，AB=AD，
不防设AB=1，则 BC=CD=BD=
| 2 |
由勾股定理的逆定理，可得AB⊥C′A．
因为AB∩AD=A，所以C′A⊥平面ABD． …（14分）
点评：本题考查面面平行，考查线面垂直，考查学生分析解决问题的能力，正确运用面面平行、线面垂直的判定定理是关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目