题目内容
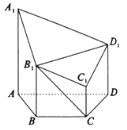
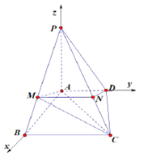
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
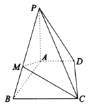
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析,(2) ![]()
【解析】
(1)作![]() 交
交![]() 于
于![]() ,通过证明四边形
,通过证明四边形![]() 为平行四边形可得到
为平行四边形可得到![]() ,根据线面平行判定定理可证得结论;
,根据线面平行判定定理可证得结论;
(2)以![]() 为坐标原点可建立空间直角坐标系,利用二面角的向量求法可求得结果.
为坐标原点可建立空间直角坐标系,利用二面角的向量求法可求得结果.
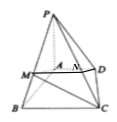
(1)由题意知:![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,则
,则![]()
作![]() 交
交![]() 于
于![]() ,连接
,连接![]()
![]()
![]()
又![]() ,
,![]() ,
,![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形 ![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
(2)由![]() 底面
底面![]() ,可得
,可得![]() ,
,![]()
又![]() ,可知
,可知![]() 两两互相垂直
两两互相垂直
以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
则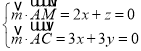 ,令
,令![]() ,得
,得![]() ,
,![]()
![]() ;
;
设平面![]() 的法向量为
的法向量为![]()
则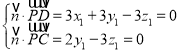 ,令
,令![]() ,得
,得![]() ,
,![]()
![]()
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,则
,则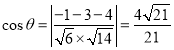
![]() 平面
平面![]() 与平面
与平面![]() 所成锐二面角的余弦值等于
所成锐二面角的余弦值等于![]()

练习册系列答案
相关题目
【题目】某市房管局为了了解该市市民![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间买二手房情况,首先随机抽样其中
月期间买二手房情况,首先随机抽样其中![]() 名购房者,并对其购房面积
名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图
)进行了一次调查统计,制成了如图![]() 所示的频率分布直方图,接着调查了该市
所示的频率分布直方图,接着调查了该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间当月在售二手房均价
月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图
(单位:万元/平方米),制成了如图![]() 所示的散点图(图中月份代码
所示的散点图(图中月份代码![]() 分别对应
分别对应![]() 年
年![]() 月至
月至![]() 年
年![]() 月).
月).

(1)试估计该市市民的购房面积的中位数![]() ;
;
(2)从该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间所有购买二手房中的市民中任取
月期间所有购买二手房中的市民中任取![]() 人,用频率估计概率,记这
人,用频率估计概率,记这![]() 人购房面积不低于
人购房面积不低于![]() 平方米的人数为
平方米的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值如下表所示:
,并得到一些统计量的值如下表所示:
|
| |
|
|
|
|
| |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出![]() 年
年![]() 月份的二手房购房均价(精确到
月份的二手房购房均价(精确到![]() )
)
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(参考公式)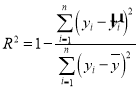 .
.