题目内容
7.将函数y=cos2x的图象向左平移$\frac{π}{4}$个单位,得到函数y=f(x)•cosx的图象,则f(x)的表达式可以是( )| A. | f(x)=-2sinx | B. | f(x)=2sinx | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin2x+cos2x) |
分析 将函数y=cos2x的图象向左平移$\frac{π}{4}$个单位,可得y=cos2(x+$\frac{π}{4}$)=cos(2x+$\frac{π}{2}$)=-sin2x=-2cosx•sinx,利用条件,可得结论.
解答 解:将函数y=cos2x的图象向左平移$\frac{π}{4}$个单位,可得y=cos2(x+$\frac{π}{4}$)=cos(2x+$\frac{π}{2}$)=-sin2x=-2cosx•sinx,
∵y=f(x)•cosx,
∴f(x)=-2sinx.
故选:A.
点评 本题考查三角函数图象变换,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
12.已知i是虚数单位.若复数z满足(1-i)•z=2i3,则复数z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
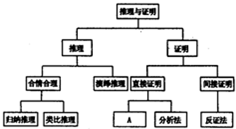 如图是教材选修1-2中《推理与证明》一章的知识结构图,请把A处填入适当的方法综合法.
如图是教材选修1-2中《推理与证明》一章的知识结构图,请把A处填入适当的方法综合法.