题目内容
y=2cosx(
sinx+cosx)的一条对称轴为( )
| 3 |
A、x=
| ||
B、x=-
| ||
C、x=-
| ||
D、x=
|
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:先根据两角和与差的正弦公式进行化简,再由正弦函数的性质2x+
=kπ+
,k∈Z,求出x的值,结合选项可得到答案.
| π |
| 6 |
| π |
| 2 |
解答:
解:∵y=2cosx(
sinx+cosx)=
sin2x+cos2x+1=2sin(2x+
)+1
∴由2x+
=kπ+
,k∈Z可解得:x=
+
,k∈Z
∴k=-1时,有x=-
故选:B.
| 3 |
| 3 |
| π |
| 6 |
∴由2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
∴k=-1时,有x=-
| π |
| 3 |
故选:B.
点评:本题主要考查两角和与差的正弦公式和正弦函数的性质,属于基本知识的考查.

练习册系列答案
相关题目
已知3x+12y=xy(x>0,y>0),则x+y的最小值为( )
| A、27 | B、21 | C、15 | D、9 |
记实数x1,x2,…,xn中的最大数为max{x1,x2,…,xn},最小数为min{x1,x2,…,xn}.已知△ABC的三边长为a,b,c(a≤b≤c),定义它的倾斜度为△ABC的l,且l=max{
,
,
}•min{
,
,
}则“l=1”是“△ABC为等边三角形”( )
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| b |
| c |
| c |
| a |
| A、必要而不充分的条件 |
| B、充分而不必要的条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
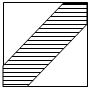 在边长为25cm的正方形中挖去腰长为23cm的两个等腰直角三角形(如图),现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是
在边长为25cm的正方形中挖去腰长为23cm的两个等腰直角三角形(如图),现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是 如图,平面内向量
如图,平面内向量