题目内容

17．在四棱锥S-ABCD中，底面ABCD是边长为a正方形，SD⊥底面ABCD，且SD=a，SA=SC=$\sqrt{2}$a．
（1）在这个四棱锥中放一个球，求球的最大半径；
（2）求四棱锥外接球的半径．

分析 （1）利用等体积法求球的最大半径；
（2）四棱锥补成长方体，求出其对角线长，即可求四棱锥外接球的半径．

解答 解：（1）由题意，求四棱锥的内切球的半径，设为r，则
由等体积可得，$\frac{1}{3}×\frac{1}{2}×a×a×a$=$\frac{1}{3}×$（a2+2×$\frac{1}{2}×a×a$+2×$\frac{1}{2}×a×\sqrt{2}a$）r，
∴r=$\frac{2-\sqrt{2}}{4}$a；
（2）四棱锥补成长方体，其对角线长为$\sqrt{3}$a，∴四棱锥外接球的半径为$\frac{\sqrt{3}}{2}$a．

点评 本题考查四棱锥内切球、外接球的半径，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
5．设log312=a，试用a表示log324．
8．已知函数f（x）=$\frac{1}{2}$x2-（a-1）x+alnx．
（1）讨论函数f（x）的单调性；
（2）证明：若1＜a＜5，则对任意x1，x2∈（0，+∞），x1≠x2，都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{ln{x}_{1}-ln{x}_{2}}$＞1．
5．在△ABC中，面积S=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{4}$，且2sinBsinC=sinA，试判断△ABC的形状．
12．若a，b＞0，且P=$\frac{\sqrt{a}+\sqrt{b}}{\sqrt{2}}$，Q=$\sqrt{a+b}$，则P、Q的大小关系是（　　）
A．P＞QB．P＜QC．P≥QD．P≤Q
2．已知logax+logcx=2logbx，且x≠1，求证：c2=（ac）${\;}^{lo{g}_{a}b}$．
9．若U=R，判断下列各运算是否正确．
（1）∁UQ∪Q=R；
（2）∁UQ∩Q=∅；
（3）∁U（∁UA）=A；
（4）∁U∅=R．
6．给出下列三个类比结论：
①若a，b，c，d∈R，复数a+bi=c+di，则a=c，b=d，类比推理出：若a，b，c，d∈Q，a+b$\sqrt{5}$=c+d$\sqrt{5}$，则a=c，b=d；
②已知直线a，b，c，若a∥b，b∥c，则a∥c，类比推理出，已知向量$\overrightarrow{a}，\overrightarrow{b}，\overrightarrow{c}$，若$\overrightarrow{a}∥\overrightarrow{b}$，$\overrightarrow{b}∥\overrightarrow{c}$，则$\overrightarrow{a}∥\overrightarrow{c}$；
③同一平面内，a，b，c是三条互不相同的直线，若a∥b，b∥c，则a∥c，类比推理出：空间中，α，β，γ是三个互不相同的平面，若α∥β，β∥γ，则α∥γ．
其中正确结论的个数是①③．
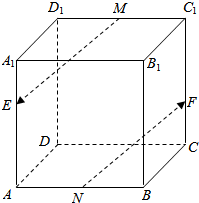7．如图，在平行六面体ABCD-A1B1C1D1中，M，N分别是C1D1，AB的中点，E在AA1上且AE=2EA1，F在CC1上且CF=$\frac{1}{2}$FC1，判断$\overrightarrow{ME}$与$\overrightarrow{NF}$是否共线？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网