题目内容
已知 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,
,
设向量 ,
,  ,
, 
(Ⅰ)若 ∥
∥ ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(Ⅱ)若 ⊥
⊥ ,边长
,边长 ,
, ,求
,求 的面积.
的面积.
 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,
,设向量
 ,
,  ,
, 
(Ⅰ)若
 ∥
∥ ,求证:
,求证: 为等腰三角形;
为等腰三角形; (Ⅱ)若
 ⊥
⊥ ,边长
,边长 ,
, ,求
,求 的面积.
的面积.(Ⅰ)利用正弦定理由角化边可以得到 ,命题即得证.(Ⅱ)
,命题即得证.(Ⅱ)
 ,命题即得证.(Ⅱ)
,命题即得证.(Ⅱ)
试题分析:证明:(1)∵m∥n∴asinA=bsinB即a•
 .其中R为△ABC外接圆半径.∴a=b∴△ABC为等腰三角形.(2)由题意,m•p=0∴a(b-2)+b(a-2)=0∴a+b=ab,由余弦定理4=a2+b2-2ab•cos
.其中R为△ABC外接圆半径.∴a=b∴△ABC为等腰三角形.(2)由题意,m•p=0∴a(b-2)+b(a-2)=0∴a+b=ab,由余弦定理4=a2+b2-2ab•cos ∴4=a2+b2-ab=(a+b)2-3ab,∴ab2-3ab-4=0,∴ab=4或ab=-1(舍去),∴S△ABC=
∴4=a2+b2-ab=(a+b)2-3ab,∴ab2-3ab-4=0,∴ab=4或ab=-1(舍去),∴S△ABC= absinC,=
absinC,=  ×4×sin
×4×sin =
=
点评:向量是数学中重要和基本的概念之一,它既是代数的对象,又是几何的对象,作为代数的对象,向量可以运算,而作为几何对象,向量有方向,可以刻画直线、平面切线等几何对象;向量有长度,可以刻画长度等几何度量问题

练习册系列答案
相关题目
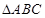 中,若
中,若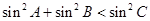 ,则
,则 与
与 的夹角为
的夹角为 。
。 及角A的大小。
及角A的大小。  ,求△ABC的面积。
,求△ABC的面积。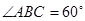 ,
,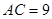 ,
,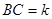 的△ABC恰有一个,那么
的△ABC恰有一个,那么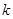 的取值范围是 ;
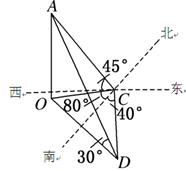
的取值范围是 ; 与两灯塔
与两灯塔 、
、 的距离分别为300米和500米,测得灯塔
的距离分别为300米和500米,测得灯塔 ,灯塔
,灯塔
 是
是 的面积,
的面积, 的对边分别为
的对边分别为 ,且
,且 ,
,