题目内容
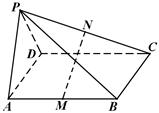
如图所示,在棱长为2的正方体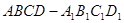 内(含正方体表面)任取一点
内(含正方体表面)任取一点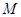 ,则
,则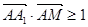 的概率
的概率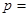 ( )
( )
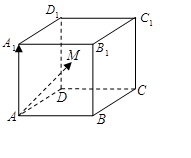
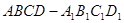 内(含正方体表面)任取一点
内(含正方体表面)任取一点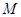 ,则
,则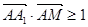 的概率
的概率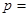 ( )
( ) 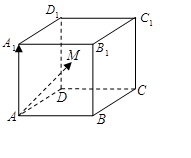
A. | B. | C. | D. |
A
试题分析:根据题意,由于在棱长为2的正方体
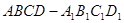 内(含正方体表面)任取一点
内(含正方体表面)任取一点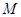 ,则
,则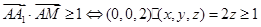 ,根据题意点Z的范围是[0,2]那么可知满足题意的概率值为
,根据题意点Z的范围是[0,2]那么可知满足题意的概率值为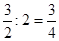 ,故答案为A.
,故答案为A.点评:主要是考查了空间向量的坐标运算,属于基础题。

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 是不同的平面,下列命题中正确的是
是不同的平面,下列命题中正确的是



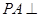 底面
底面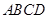 ,且PA=AB.
,且PA=AB.
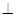 平面PAC;
平面PAC;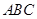 中,
中,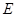 、
、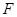 、
、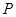 分别是
分别是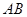 、
、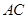 、
、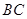 边上的点,满足
边上的点,满足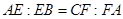
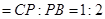 (如图1).将△
(如图1).将△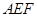 沿
沿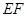 折起到
折起到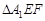 的位置,使二面角
的位置,使二面角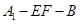 成直二面角,连结
成直二面角,连结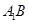 、
、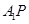 (如图2)
(如图2)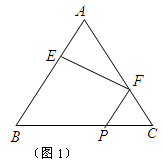
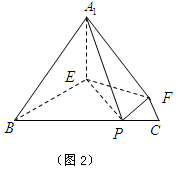
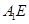 ⊥平面
⊥平面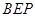 ;
;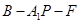 的余弦值.
的余弦值.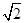 ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.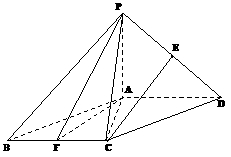
 中,
中,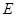 是
是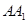 的中点.
的中点.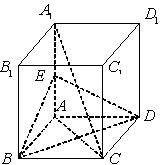
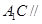 平面
平面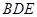 ;
;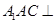 平面
平面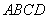 的边长为
的边长为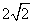 ,将
,将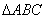 沿对角线
沿对角线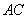 折起,使平面
折起,使平面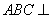 平面
平面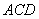 ,得到如图所示的三棱锥
,得到如图所示的三棱锥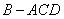 .若
.若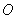 为
为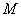 ,
, 分别为线段
分别为线段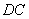 ,
,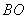 上的动点(不包括端点),且
上的动点(不包括端点),且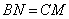 .设
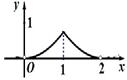
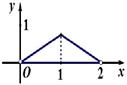
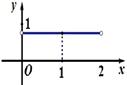
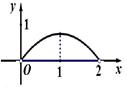
.设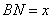 ,则三棱锥
,则三棱锥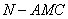 的体积
的体积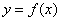 的函数图象大致是
的函数图象大致是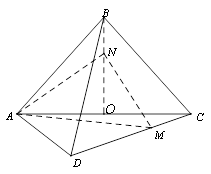
 是两条异面直线,
是两条异面直线, 是两个不同平面,
是两个不同平面, ,
, ,
, ,则
,则 与
与 至少与
至少与 .证明:平面PAD⊥平面PDC.
.证明:平面PAD⊥平面PDC.