题目内容
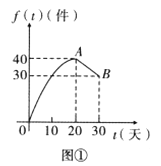
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象: 
(1)写出函数f(x),x∈R的增区间并将图象补充完整;
(2)写出函数f(x),x∈R的解析式;
(3)若函数g(x)=f(x)﹣4ax+2,x∈[1,3],求函数g(x)的最小值.
【答案】
(1)解:如图,根据偶函数的图象关于y轴对称,可作出f(x)的图象,,
则f(x)的单调递增区间为(﹣1,0),(1,+∞)

(2)解:令x>0,则﹣x<0,∴f(﹣x)=x2﹣2x
∵函数f(x)是定义在R上的偶函数,
∴f(x)=f(﹣x)=x2﹣2x
∴解析式为f(x)= ![]()
(3)解:g(x)=x2﹣2x﹣4ax+2,对称轴为x=2a+1,
当2a+1≤1时,g(1)=1﹣4a为最小;
当1<2a+1≤3时,g(2a+1)=﹣4a2﹣4a+1为最小;
当2a+1>3时,g(3)=5﹣12a为最小;
∴g(x)min= 
【解析】(1)根据偶函数的图象关于y轴对称,可作出f(x)的图象,由图象可得f(x)的单调递增区间;(2)令x>0,则﹣x<0,根据条件可得f(﹣x)=x2﹣2x,利用函数f(x)是定义在R上的偶函数,可得f(x)=f(﹣x)=x2﹣2x,从而可得函数f(x)的解析式;(3)先求出抛物线对称轴x=2a﹣﹣1,然后分当2a+1≤1时,当1<2a+1≤2时,当2a+1>2时三种情况,根据二次函数的增减性解答.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案【题目】稳定房价是我国今年实施宏观调控的重点,国家最近出台的一系列政策已对各地的房地产市场产生了影响.北京市某房地产介绍所对本市一楼群在今年的房价作了统计与预测:发现每个季度的平均单价y(每平方米面积的价格,单位为元)与第x季度之间近似满足:y=500sin(ωx+)+9500 (>0),已知第一、二季度平均单价如下表所示:
x | 1 | 2 | 3 |
y | 10000 | 9500 | ? |
则此楼群在第三季度的平均单价大约是 ( )
A.10000元
B.9500元
C.9000元
D.8500元