题目内容
(14分) 如图,在三棱柱![]() 中,四边形
中,四边形![]() 是正方形,
是正方形,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 是
是![]() 上的一点.
上的一点.
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() .
.

解析:(1)连接![]() ,∵四边形
,∵四边形![]() 是正方形,∴
是正方形,∴![]()
∵![]() ,
,![]() ,
,
∴![]() …………………………………………2分
…………………………………………2分
又![]() ,∴
,∴![]() ………………4分
………………4分
∵![]() ,∴
,∴![]() …………………6分
…………………6分
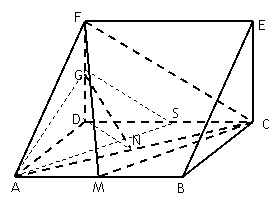
(2)取![]() 中点
中点![]() ,连接
,连接![]() ………8分
………8分
∵![]() 是
是![]() 的中点, ∴
的中点, ∴![]()
又![]()
∴![]() ……………………………………………10分
……………………………………………10分
而![]() ,∴平面
,∴平面![]() //平面
//平面![]() ……………………………………………12分
……………………………………………12分
∵ ![]() , ∴
, ∴![]() …………………………………………14分
…………………………………………14分

练习册系列答案
相关题目
(本小题满分14分) 如图:在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直(图1),图2为该四棱锥的主视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形.
|

|
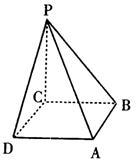
(1)根据图2所给的主视图、侧视图画出相应的俯视图,并求出该俯视图所在的平面图形的面积.
(2)图3中,L、E均为棱PB上的点,且![]() ,
,![]() ,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
,M、N分别为棱PA 、PD的中点,问在底面正方形的对角线AC上是否存在一点F,使EF//平面LMN. 若存在,请具体求出CF的长度;若不存在,请说明理由.
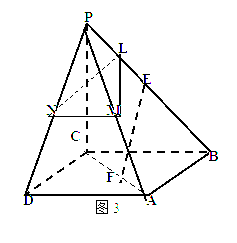
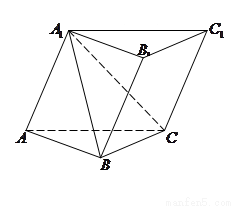
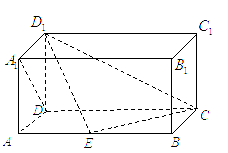 如图,在长方体
如图,在长方体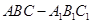 中,所有的棱长都为2,
中,所有的棱长都为2,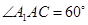 .
.
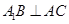 ;
; 与平面
与平面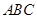 所成的锐角的余弦值.
所成的锐角的余弦值.
 B
B