题目内容
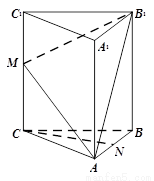
(本小题共14分)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.
(Ⅰ)求证:CN⊥AB1;
(Ⅱ)求证:CN //平面AB1M.

证明:(Ⅰ)因为三棱柱ABC-A1B1C1中CC1⊥底面ABC,
所以BB1⊥平面ABC, 所以BB1⊥CN.…………………1分
因为AC=BC,N是AB的中点,
所以CN⊥AB. ……………………3分
因为AB∩BB1=B, ……………………4分
所以CN⊥平面AB B1A1. ……………………5分
所以CN⊥AB1. ……………………6分
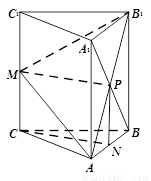 (Ⅱ)(方法一)连结A1B交AB1于P. ……………………7分
(Ⅱ)(方法一)连结A1B交AB1于P. ……………………7分
因为三棱柱ABC-A1B1C1,
所以P是A1B的中点.
因为M,N分别是CC1,AB的中点,
所以NP // CM,且NP = CM, ……………………9分
所以四边形MCNP是平行四边形, ……………………10分
所以CN//MP. ……………………11分
因为CN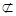 平面AB1M,MP
平面AB1M,MP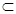 平面AB1M, ………………12分
平面AB1M, ………………12分
所以CN //平面AB1M. ……………………14分
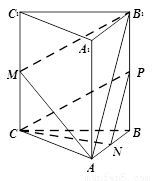
(方法二)取BB1中点P,连结NP,CP. ……………………7分
因为N,P分别是AB,BB1的中点,
所以NP //AB1.
因为NP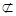 平面AB1M,AB1
平面AB1M,AB1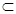 平面AB1M,
平面AB1M,
所以NP //平面AB1M. ……………………10分
同理 CP //平面AB1M. ……………………11分
因为CP∩NP =P,
所以平面CNP //平面AB1M. ……………………13分
因为CN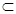 平面CNP,
平面CNP,
所以CN //平面AB1M. ……………………14分
【解析】略



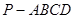 中,底面
中,底面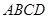 为平行四边形,
为平行四边形,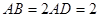 ,
,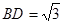 ,
, ⊥底面
⊥底面
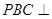 平面
平面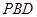 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。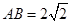 ,CC1=4,M是棱CC1上一点.
,CC1=4,M是棱CC1上一点.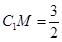 ,求二面角A-MB1-C的大小.
,求二面角A-MB1-C的大小.