Question

6．对于任意实数a，b，定义max{a，b}=$\left\{\begin{array}{l}{a}&{a≥b}\\{b}&{a＜b}\end{array}\right.$，已知在[-4，4]上的奇函数f（x）满足：当0＜x≤4时，f（x）=max{2^x-1，2-x}，若方程f（x）-mx²+1=0恰有两个根，则m的取值范围是（　　）

• A． [-$\frac{7}{8}$，0）∪（$\frac{{e}^{2}1{n}^{2}2}{4}$，1]
• B． [-$\frac{7}{8}$，0）∪（$\frac{1}{e}$，1]
• C． （-1，-$\frac{7}{8}$）∪（$\frac{{e}^{2}1{n}^{2}2}{4}$，2]
• D． （-1，0）∪（$\frac{1}{e}$，1]

Answer 1

分析 先根据条件得出函数在（0，4]上的解析式f（x）$\left\{\begin{array}{l}{2-x，0＜x＜1}\\{2^x-1，1≤x≤4}\end{array}\right.$，再运用分类讨论和数形结合的方法确定零点和m的范围．

解答 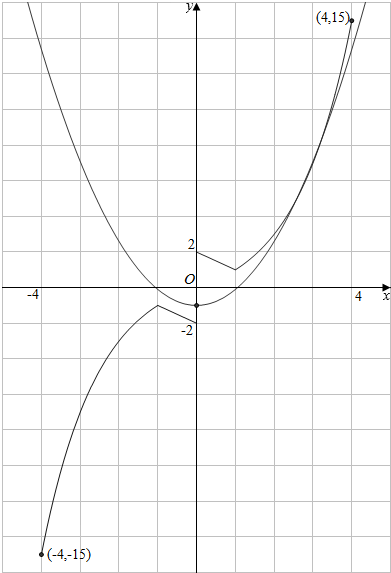解：根据定义，当x∈（0，4]时，f（x）=max{2^x-1，2-x}=$\left\{\begin{array}{l}{2-x，0＜x＜1}\\{2^x-1，1≤x≤4}\end{array}\right.$，
方程f（x）-mx²+1=0化为f（x）=mx²-1，记g（x）=mx²-1，分类讨论如下：
①当m＞0时，g（x）的图象为开口向上的抛物线，
根据几何关系，g（x）的图象只与f（x）图象在y轴右边有公共点，如下图：
根据题意，方程：2^x-1=mx²-1在（1，4]有两个交点，
分离参数得，m=$\frac{2^x}{x^2}$=h（x），令h'（x）=$\frac{2^x（xln2-2）}{x^3}$=0，解得x=$\frac{2}{ln2}$∈（2，3），
显然，当x=$\frac{2}{ln2}$时，h（x）_min=h（$\frac{2}{ln2}$）=$\frac{e^2ln^22}{4}$，且h（1）=2，h（2）=1，
要使原方程有两个实根，则$\frac{e^2ln^22}{4}$＜m≤1；
几何意义：m=$\frac{e^2ln^22}{4}$时，两图象相切；m=1时，g（x）图象过点（4，15）．
②当m＜0时，g（x）的图象为开口向下的抛物线，
根据几何关系，g（x）的图象只与f（x）图象在y轴左边有公共点，
即方程f（x）-mx²+1=0在[-4，0）恰有两根，
若x=-4为方程的根，则f（-4）-16m+1=0，解得m=-$\frac{7}{8}$，
所以，由图可知，m∈[-$\frac{7}{8}$，0），
综合以上讨论得，m∈[-$\frac{7}{8}$，0）∪（$\frac{e^2ln^22}{4}$，1]，
故选：A．

点评 本题主要考查了函数零点的判定，涉及奇函数与分段函数的图象与性质，运用了换元法，分离参数法和数形结合的解题思想，属于难题．