题目内容
15．sin22.5°•cos22.5°=$\frac{\sqrt{2}}{4}$．分析 利用倍角公式及特殊角的三角函数值即可求值得解．
解答 解：sin22.5°•cos22.5°=$\frac{1}{2}$sin45°=$\frac{\sqrt{2}}{4}$．
故答案为：$\frac{\sqrt{2}}{4}$．
点评 本题主要考查了倍角公式及特殊角的三角函数值的应用，考查了计算能力，属于基础题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
设$\frac{π}{4}$＜α$＜\frac{π}{2}$，角α的正弦线、余弦线和正切线的数量分别为a，b，c，由图比较a，b，c的大小；如果$\frac{π}{2}$＜α＜$\frac{3π}{4}$，则a，b，c的大小关系又如何？（作图并有比较的过程）
6．对于任意实数a，b，定义max{a，b}=$\left\{\begin{array}{l}{a}&{a≥b}\\{b}&{a＜b}\end{array}\right.$，已知在[-4，4]上的奇函数f（x）满足：当0＜x≤4时，f（x）=max{2x-1，2-x}，若方程f（x）-mx2+1=0恰有两个根，则m的取值范围是（ ）
| A． | [-$\frac{7}{8}$，0）∪（$\frac{{e}^{2}1{n}^{2}2}{4}$，1] | B． | [-$\frac{7}{8}$，0）∪（$\frac{1}{e}$，1] | ||
| C． | （-1，-$\frac{7}{8}$）∪（$\frac{{e}^{2}1{n}^{2}2}{4}$，2] | D． | （-1，0）∪（$\frac{1}{e}$，1] |
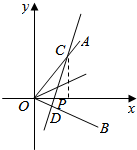如图，射线OA，OB与x轴的正方向分别成45°与30°的角，过点P（1，0）的直线与两射线分别交于C，D，若线段CD的中点恰好在直线y=$\frac{1}{2}$x上，求CD所在直线的方程．