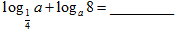题目内容
14．（1）已知f（x）=x2-2（1-a）x+2在（-∞，4]上是减函数，求实数a的取值范围．（2）已知f（x）=x2-2（1-a）x+2的单调递减区间为（-∞，4]，求实数a的值．
分析 （1）利用二次函数的单调性，求解实数a的取值范围．
（2）利用函数的单调区间，直接求解a的值即可．
解答 解：（1）f（x）=x2-2（1-a）x+2在（-∞，4]上是减函数，
二次函数的对称轴为：x=1-a，开口向上．
可得1-a≥4，解得a≤-3．
实数a的取值范围：（-∞，-3]．
（2）f（x）=x2-2（1-a）x+2的单调递减区间为（-∞，4]，
二次函数的对称轴为：x=1-a，开口向上．
1-a=4，解得a=-3．
点评 本题考查二次函数的性质的应用，函数的单调区间以及单调性的区别，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
4．已知$\overrightarrow{a}$=$\overrightarrow{e}$1+2$\overrightarrow{e}$2，$\overrightarrow{b}$=3$\overrightarrow{e}$1-4$\overrightarrow{e}$2，且$\overrightarrow{e}$1，$\overrightarrow{e}$2共线，则$\overrightarrow{a}$与$\overrightarrow{b}$（ ）
| A． | 共线 | B． | 不共线 | ||
| C． | $\overrightarrow{e}$1，$\overrightarrow{e}$2中必须有零向量才共线 | D． | 不能确定 |
5．设奇函数f（x）在（0，+∞）上是减函数，且f（π）=0，则不等式$\frac{f（x）-f（-x）}{x}$＜0的解集是（ ）
| A． | （-π，0）∪（π，+∞） | B． | （-∞，-π）∪（0，π） | C． | （-∞，-π）∪（π，+∞） | D． | （-π，0）∪（0，π） |
9．已知f（x）是R上的增函数，若a+b≥0，则有（ ）
| A． | f（a）+f（b）＞f（-a）+f（-b） | B． | f（a）+f（b）≥f（-a）+f（-b） | C． | f（a）+f（b）＜f（-a）+f（-b） | D． | f（a）+f（b）≤f（-a）+f（-b） |
19．不等式2x＞${（\frac{1}{2}）}^{x-x^2}$的解集为（ ）
| A． | （-∞，0）∪（2，+∞） | B． | （-∞，0）∪（0，+∞） | C． | （0，2） | D． | [0，2] |
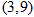在函数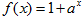
的图像上，则