题目内容
5.设奇函数f(x)在(0,+∞)上是减函数,且f(π)=0,则不等式$\frac{f(x)-f(-x)}{x}$<0的解集是( )| A. | (-π,0)∪(π,+∞) | B. | (-∞,-π)∪(0,π) | C. | (-∞,-π)∪(π,+∞) | D. | (-π,0)∪(0,π) |
分析 利用函数是奇函数,不等式$\frac{f(x)-f(-x)}{x}$<0等价为$\left\{\begin{array}{l}{x>0}\\{f(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)>0}\end{array}\right.$,然后根据函数单调性的性质解不等式即可.
解答 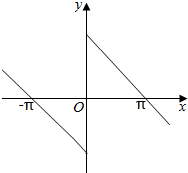 解:∵奇函数f(x)在(0,+∞)上是减函数,且f(π)=0,
解:∵奇函数f(x)在(0,+∞)上是减函数,且f(π)=0,
∴函数f(x)在(-∞,0)上是减函数,且f(-π)=-f(π)=0,
则f(x)的图象如图:
∵f(x)是奇函数,
∴不等式$\frac{f(x)-f(-x)}{x}$<0等价为$\frac{2f(x)}{x}<0$,即$\left\{\begin{array}{l}{x>0}\\{f(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)>0}\end{array}\right.$.
即$\left\{\begin{array}{l}{x>0}\\{x>π}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{x<-π}\end{array}\right.$,
即x>π或x<-π,
即不等式的解集为(-∞,-π)∪(π,+∞),
故选:C.
点评 本题主要考查函数奇偶性和单调性的应用,利用函数取值的变化即可求出不等式的解集,考查函数性质的综合应用.

练习册系列答案
相关题目
15.已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=-$\frac{1}{f(x)}$;②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex-$\frac{1}{x}$,设a=f(-5),b=f($\frac{19}{2}$),c=f($\frac{41}{4}$),则a,b,c的大小关系( )
| A. | b<a<c | B. | c<a<b | C. | b<c<a | D. | a<b<c |
16.设(x)的定义域为(-2,2),f($\frac{x}{2}$)+f($\frac{2}{x}$)的定义域为( )
| A. | (-4,0)∪(0,4) | B. | (-4,-1)∪(1,4) | C. | (-2,-1)∪(1,2) | D. | (-4,-2)∪(2,4) |
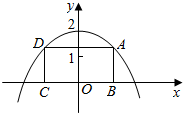 如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.