题目内容
18．直线4x+y+1=0的倾斜角α=π-arctan4．分析 先求出直线的斜率，从而求出直线的倾斜角．
解答 解：由4x+y+1=0，
得：y=-4x-1，
∴k=-4，
∴的倾斜角α=π-arctan4，
故答案为：π-arctan4．
点评 本题考查了求直线的倾斜角问题，是一道基础题．
练习册系列答案
相关题目
8．双曲线${x^2}-\frac{y^2}{m}=1$的离心率大于$\sqrt{2}$，则（ ）
| A． | $m＞\frac{1}{2}$ | B． | m≥1 | C． | m＞1 | D． | m＞2 |
9．已知f（2x-1）=x2+x，则f（5）的值为（ ）
| A． | 30 | B． | 12 | C． | 6 | D． | 9 |
6．下列命题中，正确是（ ）
| A． | 两个向量相等，则它们的起点相同，终点也相同 | |
| B． | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| C． | 四边形ABCD中，一定有$\overrightarrow{AB}$=$\overrightarrow{DC}$ | |
| D． | 若$\overrightarrow{m}$=$\overrightarrow{n}$，$\overrightarrow{n}$=$\overrightarrow{p}$，则$\overrightarrow{m}$=$\overrightarrow{p}$ |
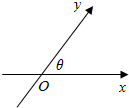如图，数轴x，y的交点为O，夹角为θ，与x轴、y轴正向同向的单位向量分别是$\overrightarrow{e_1}，\overrightarrow{e_2}$．由平面向量基本定理，对于平面内的任一向量$\overrightarrow{OP}$，存在唯一的有序实数对（x，y），使得$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$，我们把（x，y）叫做点P在斜坐标系xOy中的坐标（以下各点的坐标都指在斜坐标系xOy中的坐标）．