题目内容
已知2f(x)+f(
)=-
(x≠0),则下列说法正确的为( )
| 1 |
| x |
| 3 |
| x |
分析:通过函数的关系求出函数的解析式,判断函数的奇偶性,判断单调区间即可得到选项.
解答:解:因为2f(x)+f(
)=-
(x≠0),…①
所以2f(
)+f(x)=-3x(x≠0),…②,
解①②得f(x)=x-
,函数满足f(-x)=-f(x),所以函数是奇函数.
又可判断出g(x)=-
在(0,+∞)上为增函数.所以函数f(x)在(0,+∞)上为增函数.
故选A.
| 1 |
| x |
| 3 |
| x |
所以2f(
| 1 |
| x |
解①②得f(x)=x-
| 2 |
| x |
又可判断出g(x)=-
| 2 |
| x |
故选A.
点评:本题考查函数的解析式的求法,函数的奇偶性与函数的单调性的综合应用,考查计算能力.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
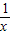 )=
)=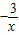 (x≠0),则下列说法正确的为( )
(x≠0),则下列说法正确的为( )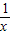 )=-
)=-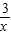 (x≠0),则下列说法正确的是( )
(x≠0),则下列说法正确的是( )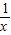 )=
)=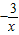 (x≠0),则下列说法正确的为( )
(x≠0),则下列说法正确的为( )