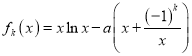题目内容
【题目】在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)上一点P![]() 到准线的距离与到原点O的距离相等,抛物线的焦点为F.
到准线的距离与到原点O的距离相等,抛物线的焦点为F.
(1)求抛物线的方程;
(2)若A为抛物线上一点(异于原点O),点A处的切线交x轴于点B,过A作准线的垂线,垂足为点E,试判断四边形AEBF的形状,并证明你的结论.
【答案】(1)y2=6x; (2) 菱形,证明见解析
【解析】
(1)由点P![]() 到准线的距离与到原点O的距离相等,可得点P在线段OF的中垂线上,进而可求p的值,即得抛物线的方程;(2)设点A在x轴的上方,设其坐标,由导函数的几何意义写出点A处的切线方程,可得到点B的坐标,进而可写出
到准线的距离与到原点O的距离相等,可得点P在线段OF的中垂线上,进而可求p的值,即得抛物线的方程;(2)设点A在x轴的上方,设其坐标,由导函数的几何意义写出点A处的切线方程,可得到点B的坐标,进而可写出![]() 与
与![]() 的坐标,进而得两向量相等,再结合抛物线定义可得AF=AE,可得四边形AEBF的形状。
的坐标,进而得两向量相等,再结合抛物线定义可得AF=AE,可得四边形AEBF的形状。
(1)由题意得点P![]() 到准线的距离等于PO,
到准线的距离等于PO,
由抛物线的定义得点P到准线的距离为PF,
所以PO=PF,即点![]() P在线段OF的中垂线上,
P在线段OF的中垂线上,
所以![]() ,p=3,
,p=3,
所以抛物线的方程为y2=6x.
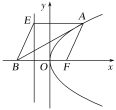
(2)四边形AEBF为菱形,理由如下:
由抛物线的对称性,设点![]() 在x轴的上方,所以点A处切线的斜率为
在x轴的上方,所以点A处切线的斜率为![]() ,
,
所以点A处切线的方程为y-y0=![]() ,
,
令上式中y=0,得x=-![]() ,
,
所以B点坐标为![]() ,
,
又![]() ,
,
所以![]()
所以![]() ,所以FA∥BE,
,所以FA∥BE,
又因为AE∥FB,故四边形AEBF为平行四边形,
再由抛物线的定义,得AF=AE,所以四边形AEBF为菱形.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目