题目内容
已知函数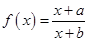 (
( 、
、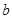 为常数).
为常数).
(1)若 ,解不等式
,解不等式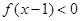 ;
;
(2)若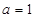 ,当
,当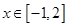 时,
时,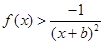 恒成立,求
恒成立,求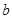 的取值范围.
的取值范围.
(1)①当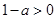 ,即
,即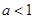 时,不等式的解集为:
时,不等式的解集为: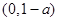
②当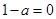 ,即
,即 时,不等式的解集为:
时,不等式的解集为: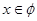
③当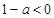 ,即
,即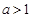 时,不等式的解集为:
时,不等式的解集为: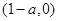 ;
;
(2)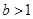 .
.
解析试题分析:(1)由不等式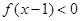 得
得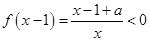 ,按照
,按照 与0的大小关系分三种情况讨论,可解不等式;
与0的大小关系分三种情况讨论,可解不等式;
(2)若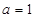 ,不等式可化为
,不等式可化为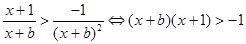 ,由
,由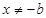 可知
可知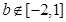 ,分离参数
,分离参数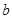 后化为函数的最值即可,由基本不等式可求得范围.
后化为函数的最值即可,由基本不等式可求得范围.
试题解析:(1)∵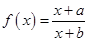 ,
, ,
,
∴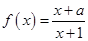 ,
,
∴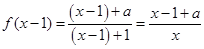 ,
,
∵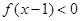 ,
,
∴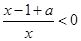 ,等价于
,等价于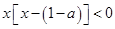 ,
,
①当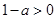 ,即
,即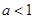 时,不等式的解集为:
时,不等式的解集为: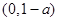 ,
,
②当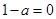 ,即
,即 时,不等式的解集为:
时,不等式的解集为: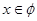 ,
,
③当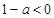 ,即
,即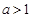 时,不等式的解集为:
时,不等式的解集为: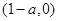 ,
,
(2)∵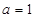 ,
,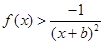 ,
,
∴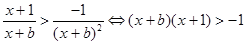 (※)
(※)
显然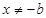 ,易知当
,易知当 时,不等式(※)显然成立;
时,不等式(※)显然成立;
由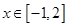 时不等式恒成立,可知
时不等式恒成立,可知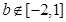 ;
;
当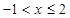 时,
时,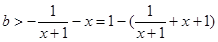 ,
,
∵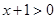 ,
,
∴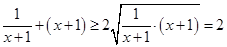 ,
,
故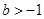 .
.
综上所述,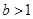 .
.
考点:1、解不等式;2、分类讨论;3、基本不等式;4、函数的恒成立问题.

练习册系列答案
相关题目
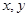 满足
满足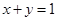 ,求
,求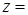
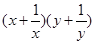 的最小值.
的最小值. ,(x>0,
,(x>0,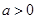 ).
).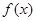 >-x+4,求实数
>-x+4,求实数 的取值范围
的取值范围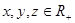 求证:
求证: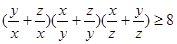
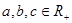 且
且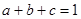 ,求证:
,求证: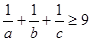
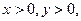 且
且 的最小值为 .
的最小值为 .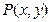 在直线
在直线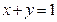 位于第一象限内的图象上运动, 则
位于第一象限内的图象上运动, 则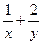 的最小值是 ____
的最小值是 ____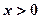 ,则
,则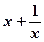 的最小值为 .
的最小值为 .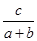 +
+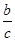 的最小值.
的最小值.