题目内容
若关于x的不等式[x-（3-a）]（x-2a）＜0的解集是A，函数y=
的定义域是B，若A∪B=A，求实数a的取值范围．
| 1 | ||
|
由-x2+3x-2＞0，得1＜x＜2．
所以B=（1，2）．
由[x-（3-a）]（x-2a）＜0得解集是A，且A∪B=A，
所以A≠∅，且B⊆A，
若a＞1，解[x-（3-a）]（x-2a）＜0，得3-a＜x＜2a，A=（3-a，2a），
由B⊆A，得
，所以a≥2；
若a＜1，解[x-（3-a）]（x-2a）＜0，得2a＜x＜3-a，A=（2a，3-a），
由B⊆A，得
，所以a≤
．
所以实数a的取值范围是a≤
或a≥2．
所以B=（1，2）．
由[x-（3-a）]（x-2a）＜0得解集是A，且A∪B=A，
所以A≠∅，且B⊆A，
若a＞1，解[x-（3-a）]（x-2a）＜0，得3-a＜x＜2a，A=（3-a，2a），
由B⊆A，得
|
|
若a＜1，解[x-（3-a）]（x-2a）＜0，得2a＜x＜3-a，A=（2a，3-a），
由B⊆A，得
|
| 1 |
| 2 |
所以实数a的取值范围是a≤
| 1 |
| 2 |
练习册系列答案
步步高达标卷系列答案
相关题目
.
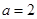时，解不等式
；
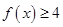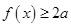恒成立，求实数
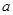的取值范围.
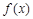是定义在R上的偶函数，在
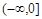上是减函数，且
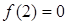，则使得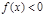
的x的取值范围是 （ ）
