题目内容
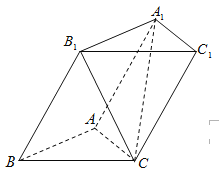
【题目】如图,![]() 中,
中,![]() ,
,![]() ,若以
,若以![]() ,
,![]() 为焦点的双曲线的渐近线经过点
为焦点的双曲线的渐近线经过点![]() ,则该双曲线的离心率为
,则该双曲线的离心率为

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
设AB=BC=2,取AB的中点为O,由题意可得双曲线的一条渐近线为直线OC,由余弦定理可得OC,cos∠COB,求得tan∠COB,即为渐近线的斜率,由a,b,c的关系和离心率公式,即可得到.
设AB=BC=2,
取AB的中点为O,
由题意可得双曲线的一条渐近线为直线OC,
在三角形OBC中,
cosB=﹣![]() ,
,
∴OC2=OB2+BC2﹣2OBBCcosB=1+4﹣2×1×2×(﹣![]() )=7,
)=7,
∴OC=![]() ,
,
则cos∠COB=![]() =
=![]() ,
,
可得sin∠COB=![]() =
=![]() ,
,
tan∠COB=![]() =
=![]() ,
,
可得双曲线的渐近线的斜率为![]() ,
,
不妨设双曲线的方程为![]() ﹣
﹣![]() =1(a,b>0),
=1(a,b>0),
渐近线方程为y=±![]() x,
x,
可得![]() =
=![]() ,
,
可得e=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
故选:D.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目